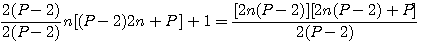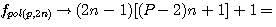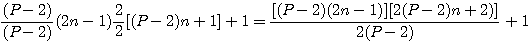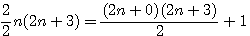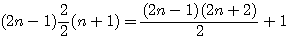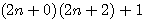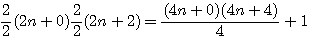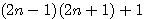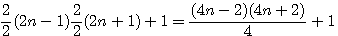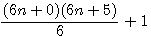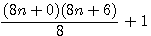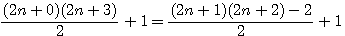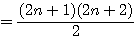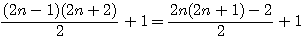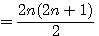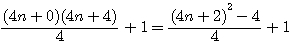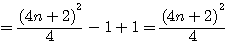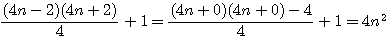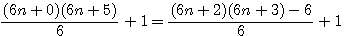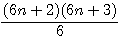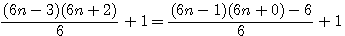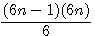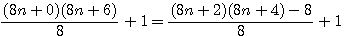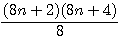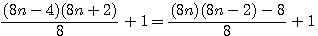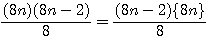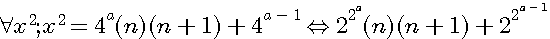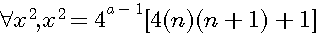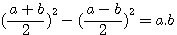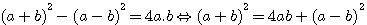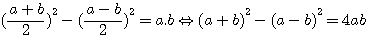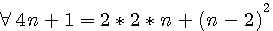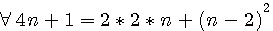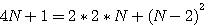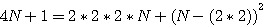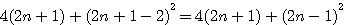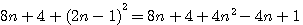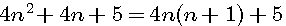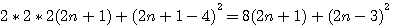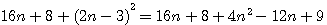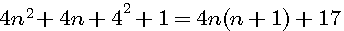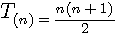
Cette page détaille les équations utilisées dans différentes pages de schemath.com . Dans chaque chapitre vous trouverez les liens de la provenance de la page concernée.
Médiane d'une serie de nombre consécutifs / Tout nombre = la différence de 2 carrés
Tout nombre est le produit de deux nombres:
Soit un nombre x , ce nombre égal x * 1 quel que soit ce nombre. Exemple 7 = 7*1 , 10 = 10*1.Si ce nombre est impair alors 2n+1 = (2n+1)*1 , si il est pair, 2n*1. Hors si ce nombre est pair alors il est aussi = à 2*n.
Médiane d'un nombre impair (donc de forme 2n+1)
La médiane du produit de ce nombre entre x et 1,dans la sequence 1,2,3,4...x = (x +1)/2 et non pas x/2
exemple x=7
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
le millieu = 4 (et non pas 3,5) c'est a dire 1,2,3 = 3 nombres consécitifs , 4 le millieu , 5,6,7 = 3 nombres consecutifs .
Donc si la forme de ce nombre est 2n+1 alors ce nombre est égal à n+1+n , la valeur de la médiane auusi appelèe "altitude" égal à (n+1); Dans l'exemple ci dessus,la representation de 7 = 2(3)+1 = 3+1+3, la valeur de chaque marche =1 , c'est à dire 1,1+1,1+1+1 ....l'altitude , la valeur, de la médiane = 1+7/2 = 1+n = 4.
|
Prenons un exemple concret . Si un escalier est composé de 7 marches , chaque marche mesurant(*) 40 cm .alors sa longueur totale = 1*40cm*7 = 2.8m.7 = 2(3)+1 = (3+1+3) * 40cm
-La largueur de chaque marche égale à 1*40cm. -Si je me tiens sur la 4ém marche , j'ai parcouru 3*40cm -Il me reste à monter 3*40cm
(*) Tous les anciens mathématiciens comme Diophante ou Euclide utilise le terme de "mesure" quand ils parlent de division. |
|
En résumé: Médiane d'un (2n+1) = 
Médiane d'un 2n
Si un nombre est pair alors la médiane entière est égale à (2n)/2 = n , hors la "largeur" de cette médiane = 0 , sa représentation étant n+0+n.Hors ma marche mesure 40cm!Exemple, Escalier de 10 marches,médiane = 5, Si je fait (5+0+5)*40 , j'aurais bien 2m+0m+2m mais si je me tiens sur la 5 elle ne mesure pas 0 cm!!!!
Si je fait : médiane = (10+1)/2 = 5,5 , mon escalier mesure 10 marches et non pas 11....
Hors il existe une solution: Si je considére un nombre pair de forme 2n comme étant aussi égal à 2(n-1) + 2, alors 2n = (n-1) + 2 + (n-1).
Donc dans mon exemple d'escalier à 10 marche , n=5 , sa représentation est égale à 4+2+4 , la longueur des 2 marches du millieu = 80cm.Il faut donc que je monte l'escalier 2 par 2 marches.... si je commence par le pallier = 2émé marche,4éme,6,8,10 , si je commence par la premère marche 1,3,5,7,9 ...
En résumé: Médiane d'un 2n= 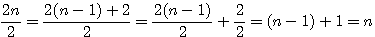
Cette expression parait stupide mais si l'on considére que n ou n-1 ou n-2 est divisible par 3 alors celà deviendra beaucoup plus interressant....
Clef de fermat N°2 : Théorème des extremes d'une factorielle
Nous avons dans la formule 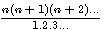 remplacer n par 1 pour calculer la somme totale des indices , mais quels sont les indices multiple de n et ceux qui ne le sont pas ?
remplacer n par 1 pour calculer la somme totale des indices , mais quels sont les indices multiple de n et ceux qui ne le sont pas ?
Dans (n+0)(n+1)(n+2) il est facile ,comme vu précédement, de calculer le dernier terme = 0*1*2 =0 donc cette expression sera du type an3+bn2+cn1,a+b+c=3!=6, somme des termes multiple de n = 6;
Si par contre j'ajoute 1 à n alors j'obtiens (n+0+1)(n+1+1)(n+1+2) = (n+1)(n+2)(n+3) , cette expression deviendra an3+bn2+cn1 + 6,somme totale des indices = 24 , indices multiple de nx = 24-6 = a+b+c = 18 ; non multiple de n=6
Si je vérifie : (n+0)(n+1)(n+2) =1n3+3n2+2n , (n+1)(n+2)(n+3)=1n3+6n2+11n+6 =>indices multiple de n = 18 , indices non multiple de n=6 , mais nous savons que Pierre de Fermat ne pouvait absolument pas développer ces expressions .
Calcul des extrêmes d'une factorielle n(n+1)(n+2)...(n+a):
Soit l'expression de nombre de facteurs pair (n+0)(n+1)(n+2)(n+3)(n+4)(n+5), calculons le produit des deux extrémités (n+0)(n+5) = n²+5n+0n+0 = n²+5n+0 = (n)(n+5) quelque soit n.
Si maintenant nous calculons dans (n+0)(n+1)(n+2)(n+3)(n+4)(n+5) : (n+1)(n+4) =n²+4n+1n+4 =n²+5n+4
Si maintenant nous calculons dans (n+0)(n+1)(n+2)(n+3)(n+4)(n+5) : (n+2)(n+3) =n²+3n+2n+6 =n²+5n+6
Quelque soit le calcul de ces facteurs les multiples de n SONT TOUJOURS EGAUX
c'est à dire dans cet exemple il est égal à 5 ou ,si l'on considère que n²+5n = 1n²+5n , égaux 1+5 = 6
Calcul des facteurs en gras |
remplacement de n par 1 |
remplacement de n par 2 |
||||
|
(n+0)(n+1)(n+2)(n+3)(n+4)(n+5) |
n(n+5) |
n²+5n+0 |
n(n+5) => 1(1+5)=6 |
= [n²+5n]+0 =>1+5=[6] |
n(n+5) =>2(2+5)=>14 |
=n²+5n+0 =>4+10=14 |
|
(n+0)(n+1)(n+2)(n+3)(n+4)(n+5) |
(n+1)(n+4) |
n²+4n+1n+4 =n²+5n+4 |
(n+1)(n+4) => (1+1)(1+4)=2*5=10 |
=n(n+5)+(1*4) =>[6]+4=10 |
(n+1)(n+4) => (2+1)(2+4)=18 |
=n(n+5)+4 =>[14]+4=18 |
|
(n+0)(n+1)(n+2)(n+3)(n+4)(n+5) |
(n+2)(n+3) |
n²+3n+2n+6 =n²+5n+6 |
(n+2)(n+3) => (1+2)(1+3)=3*4=12 |
=n(n+5)+(2*3) =>[6]+6=12 |
(n+2)(n+3) => (2+2)(2+3)=4*5=20 |
=n(n+5)+6 =>[14]+6=20 |
Nous remarquons que dans une expression du genre (n+a)(n+b) il nous suffit de retrancher a*b pour obtenir une expression n[n+(a+b)]
exemple : (n+5)(n+10) - 50 = n(n+15) , remplaçons n par 10 pour vérifier , 15*20 = 300 , 300-50 = 250 = 10*25
Soit l'expression de nombre de facteurs impair (n+0)(n+1)(n+2)(n+3)(n+4)(n+5)(n+6), calculons le produit des deux extrémités (n+0)(n+6) = n²+6n+0n+0 = n²+6n+0 = (n)(n+6) quelque soit n.
Si maintenant nous calculons dans (n+0)(n+1)(n+2)(n+3)(n+4)(n+5)(n+6) : (n+1)(n+5) =n²+5n+1n+5 =n²+6n+5
Si maintenant nous calculons dans (n+0)(n+1)(n+2)(n+3)(n+4)(n+5)(n+6) : (n+2)(n+4) =n²+4n+2n+8 =n²+6n+8
Si maintenant nous calculons dans (n+0)(n+1)(n+2)(n+3)(n+3)(n+4)(n+5)(n+6) : (n+2)(n+4) =n²+4n+2n+8 =n²+6n+9
Nous nous intéresserons, dans les paragraphes suivants, à : (n+2)(n+4) +1 = (n+3)²
Calcul des facteurs en gras |
remplacement de n par 1 |
remplacement de n par 2 |
||||
|
(n+0)(n+1)(n+2)(n+3)(n+4)(n+5)(n+6) |
n(n+6) |
n²+6n+0 |
n(n+6) => 1(1+6)=7 |
= [n²+6n]+0 =>1+6=[7] |
n(n+6) =>2(2+6)=>16 |
=n²+6n+0 =>4+12=16 |
|
(n+0)(n+1)(n+2)(n+3)(n+4)(n+5)(n+6) |
(n+1)(n+5) |
n²+5n+1n+5 =n²+6n+5 |
(n+1)(n+5) => (1+1)(1+5)=2*6=12 |
=n(n+6)+(1*5) =>[7]+5=12 |
(n+1)(n+5) => (2+1)(2+5)=21 |
=n(n+6)+5 =>[16]+5=21 |
|
(n+0)(n+1)(n+2)(n+3)(n+4)(n+5)(n+6) |
(n+2)(n+4) |
n²+4n+2n+8 =n²+6n+8 |
(n+2)(n+4) => (1+2)(1+4)=3*5=15 |
=n(n+6)+(2*4) =>[7]+8=15 |
(n+2)(n+4) => (2+2)(2+4)=24 |
=n(n+6)+8 =>[16]+8=24 |
|
(n+0)(n+1)(n+2)(n+3)²(n+4)(n+5)(n+6) |
(n+3)(n+3) |
=n²+6n+9 |
(n+3)² => (1+3)²=16 |
=[n²+6n]+3² =>[7]+9=16 |
(n+3)² => (2+3)²=25 |
=n(n+6)+3² =>[16]+9=25 |
Généralisations :
|
(n+a)(n+b)= n² + an + bn + ab = n² + n(a+b) + ab et aussi (n+0)(n+(a+b))=n²+(a+b)n+0 donc (n+a)(n+b)-ab=(n+0)(n+(a+b)) si l'on ajoute à (n+a) le même nombre
[ n + (a+ notez la factorisation de (a+ |
Carré d'un nombre de la forme 2n+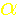
Soit un nombre 2n+![]() = n+(n+
= n+(n+![]() ) , la difference de ces 2 termes =(n+
) , la difference de ces 2 termes =(n+![]() )-
)-![]() =
=![]() , par exemple 5+(5+3) =5+8 , 8-5=3.
, par exemple 5+(5+3) =5+8 , 8-5=3.
Ce nombre au carré = (2n+![]() )² = 4n²+4n
)² = 4n²+4n![]() +
+![]() ² , si l'on factorise les 2 premiers termes par 4n alors (2n+
² , si l'on factorise les 2 premiers termes par 4n alors (2n+![]() )² = 4n(n+
)² = 4n(n+![]() )+
)+![]() ²
²
|
(2n+ |
(2n+![]() )² = 4n²+4n
)² = 4n²+4n![]() +
+![]() ² , si l'on factorise les 2 premiers termes par 2n alors (2n+
² , si l'on factorise les 2 premiers termes par 2n alors (2n+![]() )² = 2n(2n+2
)² = 2n(2n+2![]() )+
)+![]() ²
²
![]() Notez que pour 1² , n=0 et
Notez que pour 1² , n=0 et ![]() =1
=1
![]() si
si ![]() = 0 alors (2n+0)² = 4(n)(n+0)+0 = 4n²
= 0 alors (2n+0)² = 4(n)(n+0)+0 = 4n²
Rapprochement de 4n(n+a)+a² et (x+y)²-(x-y)²=4ab
Soit la formule (2n+![]() )² = 4n(n+
)² = 4n(n+![]() )+
)+![]() ² et la formule de Diophante
² et la formule de Diophante 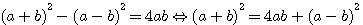 , si a=n et b=(n+
, si a=n et b=(n+![]() ):
):
|
(a+b)² |
= |
4ab |
+ |
(a-b)² <=> (b-a)² |
|
<=> |
<=> |
|||
|
[n+(n+ |
= |
4(n)(n+ |
+ |
|
Pourquoi s'intéresser qu'aux carrés impair?
Carrés pair dans (2n+![]() )² = 4n(n+
)² = 4n(n+![]() )+
)+![]() ²
²
Soit x un nombre pair , il aura la forme 2n , son carré = 2²n² , si n est lui même pair alors son carré = 2²2²n'² et ainsi de suite jusqu'a ce que n soit impair dans tous les cas de figures
Par exemple 6 = 2*3 , 6² = 2²*3² , meme 2² = 2(1) = 2²1²
Dans l'équation (2n+![]() )² = 4n(n+
)² = 4n(n+![]() )+
)+![]() ² , si (2n+
² , si (2n+![]() ) est pair alors (2n+
) est pair alors (2n+![]() )²= 2²2²2²(4n'(n'+
)²= 2²2²2²(4n'(n'+![]() ')+
')+![]() '²)
'²)
Carrés pairs dans (a+b)²-(a-b)²=4ab
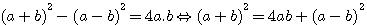 , 4ab=4ab que si (a+b) et (a-b) impair sinon l'on obtient
, 4ab=4ab que si (a+b) et (a-b) impair sinon l'on obtient 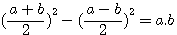
Carré impair
Soit la formule (2n+![]() )² = 4n(n+
)² = 4n(n+![]() )+
)+![]() ² si (2n+
² si (2n+![]() )² est impair alors
)² est impair alors ![]() 2 à la forme (2a+1)2, c'est à dire que l'on remplace
2 à la forme (2a+1)2, c'est à dire que l'on remplace ![]() par 2a+1
par 2a+1
|
Théorème: Tout (2N+1)² est égal à 4(N)(N+1)+1² = 4n(n+2a+1) + (2a+1)² |
|
si a=0 alors (2N+1)² = 4(n)(n+2(0)+1) +1²= 4(n)(n+1)+1 N=(n+a) 2N+1 étant égal à la somme des facteurs de (n) et (n+2a+1) alors 2N+1 = n+(n+2a+1) =2n+2a+1=2(n+a)+1
Exemple N=7 , 2N+1 = 2(3)+1, (2N+1)²=4(3)(4)+1² =7². 7= 2(2+1)+1
|
Exemple en tableau de la formule 4n(n+2a+1) + (2a+1)² |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
(2(n+a)+1)² = 4n(n+2a+1) + (2a+1)² |
![]() L'intervalle entre n et (2a+n+1) =2a
L'intervalle entre n et (2a+n+1) =2a
![]() n(n+2a+1) divisible par 2 donc 4n(n+2a+1) divisible par 8
n(n+2a+1) divisible par 2 donc 4n(n+2a+1) divisible par 8
Exercise: Soit 8(n) un nombre, quel est le carré impair à rajouter ?
Si ce nombre est de type 8n c'est que n est impair sinon il serait 8(2n) = 16n
8n = 4*2*n la difference entre n et 2 = n-2. il faut rajouter (n-2)² pour obtenir
soit ; 4n(n+2a+1) + (2a+1)² ,n-2 = 2a+1 => 4n(n+n-2)+(n-2)²=>4n(2n-2)+(n-2)²=>8(n)(n-1)+(n-2)²
exemple 8(7) = 56 = 4*2*7 , 7-2 = 5² , 56+25 = 81 = 9²
Egalité entre [2(n+a)+1)]² et x²-y²
Soit un carré x² = (x²-y²)+y²=(x-y)(x+y)+y² , si x est impair il a la forme 2n+1 alors dans (x-y)(x+y)+y² si x=2n+1 et y=1 => (2n+1)² = (2n+1-1)(2n+1+1)+1² => (2n+1)² = (2n)(2n+2)+1² , si y=2 alors (2n+1)²=(2n-1)(2n+3)+2² , si y=3 alors (2n+1)²=(2n-2)(2n+4)+3²
Pour connaitre le carré rajouté il faut prendre la valeur absolue des nombres ajoutés à 2n et les diviser par 2
Exemple (2n+1)²=(2n-2)(2n+4)+3² , 2+4 =6 ,6/2 = 3....
|
(2n+1)² = (2n+1-y)(2n+1+y)+y² |
Si dans (x-y)(x+y)+y² , y² est impair (y est donc impair) :
Les 2 facteurs du produit (2n+1-y)(2n+1+y) sont factorisables par 2 , exemple (2n-2)(2n+4)+3² = 4(n-1)(n+2)+3²
La valeur absolue de la somme des 2 nombres =y
Si y = 2a+1 alors:
(2n+1)² = (2n+1-y)(2n+1+y)+y² => (2n+1)²=[(2n+1)-(2a+1)] [(2n+1)+(2a+1)]+(2a+1)² => (2n+1)²= [2(n-a)][2(n+a)+2)+(2a+1)²=>
|
pour tout n & a ( 2n+1 )² = 4(n-a)(n+a+1)+(2a+1)² |
exemple n=4 a=1 , 9²=4(3)(6)+3² , si n=1 a=4 alors 3²=4(-3)(6)+81 = 81-72=9
Si n=n+a alors :( 2n+1 )² = 4(n-a)(n+a+1)+(2a+1)² = (2(n+a)+1)² = 4n(n+2a+1) + (2a+1)²
|
Pour résumer: ( 2n+1 )² = 4(n-a)(n+a+1)+(2a+1)² = n est une somme de 2 nombres n'+a (2n+1)² = (2(n'+a)+1)² = 4n'(n'+2a+1) + (2a+1)² |
Hypothénuses
Dans la page ![]() nous aboutissons aux
formules suivantes:
nous aboutissons aux
formules suivantes:
( 2n+1 )² = 4(n-a)(n+a+1)+(2a+1)²
=
n est une somme de 2 nombres n'+a
![]()
(2n+1)² = (2(n'+a)+1)² = 4n'(n'+2a+1) + (2a+1)²
|
|
Soit un nombre polygonal , trouver le coté = Racine Polygonale
Orientation de mes recherches:
Dans ma recherche sur l'étude des nombres polygonaux de Pierre de Fermat outre toutes les théories énoncées ci-dessus , Nombres de forme 2n ou 2n+1 selon sa parité (voir paragraphe précédent) et les factorielles, il y a un élément fondamental qui a attiré mon attention et mon incomprehension la plus totale:
La formule des nombre polygonaux utilisée par Diophante est : 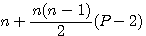 alors que Pierre de Fermat utilise la formule
alors que Pierre de Fermat utilise la formule 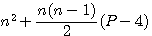 , cette formule si le polygone à 4 cotés (c'est a dire P=4) donne n² = n² ce qui à priori n'abouti à rien... (je vous suggère de suivre ce lien pour un petit rappel)
, cette formule si le polygone à 4 cotés (c'est a dire P=4) donne n² = n² ce qui à priori n'abouti à rien... (je vous suggère de suivre ce lien pour un petit rappel)
Je vous rappelle aussi qu'un nombre triangulaire est aussi un autre cas particulier , si l'on remplace P par 3 alors T(n) = n(n+1)/2 , T(n)= à la somme des nombres de 1 a n
Quoi qu'il en soit dans ces deux formule : Polygonal (n) de coté P = 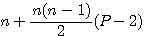 ou =
ou = 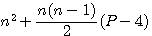 ,le gros problème est que ,pour trouver le coté d'un nombre polygonal ,c'est à dire n, il faut retirer à ce nombre un nombre n ou un nombre n² , puis trouver ce nombre n...
,le gros problème est que ,pour trouver le coté d'un nombre polygonal ,c'est à dire n, il faut retirer à ce nombre un nombre n ou un nombre n² , puis trouver ce nombre n...
Si pour un nombre triangulaire T ,ce nombre est facile à trouver avec la formule ,qui est , je le rappelle un cas particulier, T(n) = n(n+1)/2 c'est une autre paire de manche pour trouver n avec pentagonal.
Polygonaux et 2n ou 2n+1:
Si dans la formule de Diophante d'un nombre polygonal d'un nombre de coté P : 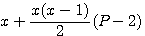 nous remplaçons x par 2n ou 2n+1 selon sa parité l'on obtient pas grand chose (je vous faut grâce de mes calculs ) par contre , si dans
nous remplaçons x par 2n ou 2n+1 selon sa parité l'on obtient pas grand chose (je vous faut grâce de mes calculs ) par contre , si dans 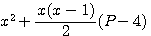 nous remplaçons x par 2n ou 2n+1 selon sa parité alors :
nous remplaçons x par 2n ou 2n+1 selon sa parité alors :
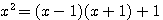 donc
donc 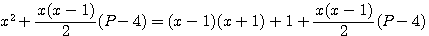 :
:
|
x est impair =2n+1 |
x est pair =2n |
|
mise au dénominateur commun de (2n)(2n+2)
Dans les deux termes divisons 2n par 2 le seul facteur commun divisible par 2
Factorisation par n :
|
mise au dénominateur commun de (2n-1)(2n+1)
Dans le premier terme 2(2n-1)(2n+1) le seul facteur divisible par 2 est 2 Dans le deuxième terme (2n)(2n-1)(P-4) , ignorant (p-4) le seul facteur divisible par 2 est 2n
donc:
Factorisation par 2n-1
|
Au vu de ces formules leurs intérêt ne saute pas immédiatement aux yeux pourtant nous pouvons dors et déjà écrire :
Premières conclusions
![]() Si un nombre NP est un nombre polygonal alors NP-1 est le produit de deux nombres, quelque soit son nombre de cotés P
Si un nombre NP est un nombre polygonal alors NP-1 est le produit de deux nombres, quelque soit son nombre de cotés P
Et donc aussi : Sauf si n=1 , NP-1 n'est pas premier
Il nous suffit donc , pour trouver le produit de ces deux nombre de retrancher 1 à n'importe quel nombre polygonal , par exemple 36 -1 = 35 = 7*5 (36 étant un nombre polygonal de 4 cotés)
![]() La somme de deux polygonaux sera égale à ab+cd+2 , la somme de trois polygonaux sera égale à ab+cd+ef+3 ...
La somme de deux polygonaux sera égale à ab+cd+2 , la somme de trois polygonaux sera égale à ab+cd+ef+3 ...
Simplification:
Si pour un polygone de 4 coté cette representation est pratique ,le terme (P-4)(2n+1) ou (P-4)(n) étant égale a zéro , elle n'est pas ,pour ma part, representative des autres polygones entre autre pour P=3 au quel cas (P-4) sera négatif, et puis cet équation est compliquée et il est très difficile d'en trouver des points communs
|
Distribution de (P-4)(2n+1)=P(2n+1)-4(2n+1)
un peu d'ordre:
distribution de P dans P(2n+1)
factorisation par 2n
|
Distribution de (P-4)(n)=Pn-4n
un peu d'ordre
factorisation par n
|
|
Tout d'abord examinons le résultat selon la valeur de P
Mise en relation avec une factorielles de Fermat: Observation de Fermat sur l'étude du problème de Diophante (question 4): Etant donné un nombre polygonal trouver le coté:
Nous avons trouvé une belle et admirable proposition que nous placerons ici sans démonstration. Dans la progression des nombres naturels commençant par l'unité, un nombre quelconque, multiplié par celui qui le suit et qui est plus grand, fait le double du triangulaire de ce nombre; La multiplication du triangulaire, par le nombre qui le suit et qui est plus grand dans la progression, donne le triple du pyramidal; Le produit du pyramidal, par le nombre suivant de la progression, donne le quadruple du triangulo--triangulaire, et ainsi à l'infini par une méthode générale et uniforme; et je ne pense pas qu'on puisse donner sur les nombres un théorème plus beau et plus général, je n'ai ni le loisir ni la convenance d'insérer la demonstration à la marge (1)
Ce que j'ai traduit par : |
Tableau des nombres Polygonaux pour n et P nombre de coté Pour p=3 le nombre obtenu est un nombre triangulaire (C.A.D Pour p=4 le nombre obtenu est un carré
Tableau obtenu avec la formule : |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Il nous faut donc transformer le Tableau précedent des deux produits +1 pour qu'il "ressemble" à la factorielle ci dessus , par exemple pour P=4,le produit de deux nombres d'un carré impair -1 étant égal à n(4n+4) est aussi = à 2n(2n+2) , donc x=2n
|
Polygonal d'un nombre impair =>2n+1
|
Polygonal d'un nombre pair =>2n
|
|||
|
Produit : |
= |
Produit : |
= |
|
| P=3 |
n(2n+3)+1 |
|
(2n-1)(n+1)+1 |
|
| P=4 |
n(4n+4)+1 |
=
|
(2n-1)(2n+1)+1 |
=
|
| P=5 |
n(6n+5)+1 |
|
(2n-1)(3n+1)+1 |
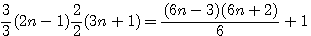 |
| P=6 |
n(8n+6)+1 |
|
(2n-1)(4n+1)+1 |
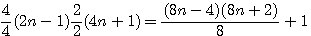 |
Exemple :
Trouvons le coté du Pentagonal (p=5) = 145 , 145 -1 =144 , que l'on multiplie par 6 ce qui sera égal 144*6 = 864 = 27*32 = (30-3)(30+2) , 2n=10 , n=5
Problématique 1 , choisir quelle fonction appliquée: Si pour un carré nous trouvons très facilement si il est issu d'un nombre de type 2n ou 2n+1 (antécédent d'un nombre 2n ou 2n+1avec p=4), le carré d'un nombre ,de type 2n, étant pair et le carré d'un nombre impair ,de type 2n+1 étant impair , par exemple le carré de 2*3+1=5 ,impair, 7²=49 , le carré de 6,6² pair, =36 pair ;ce qui nous permet de choisir la bonne somme du tableau si dessus . Ce n'est pas le cas d'autres polygonaux , triangulaires, pentagonaux ....
Problématique 2 , choisir les deux "bon" facteurs : Pour un carré nous trouvons le coté facilement, et pour un nombre triangulaire c'est , en appliquant la formule simplifiée (n)(n+1)/2 , il est facile d'en extrapoler les deux facteurs consécutifs (exemple T(5)15 , *2 = 30 = 5*6), l'on voit que cela est une autre paire de manche pour un pentagonal ...
Exemple : trouver le coté d'un pentagonal (P=5) = 145 - 1 = 144 *6 = 12*12*6 = (3*3*3)(4*4*2)=27*32 = (6*5-3)(6*5+2) , n=5 vraiment pas facile
Pour résoudre ces deux problématiques , utilisons le théorème des deux extrêmes:
rappel : 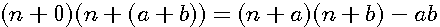 appliquons au tableau en modifiant a et b de telle sorte que -ab soit égal au diviseur :
appliquons au tableau en modifiant a et b de telle sorte que -ab soit égal au diviseur :
Soit x est un polygonal de coté p, trouver le coté
|
Polygonal d'un nombre impair =>2n+1
|
Polygonal d'un nombre pair =>2n
|
|||
|
dividende |
= |
|
= |
|
| P=3 |
|
|
|
|
| P=4 |
16n²+16n= (4n)²+2*4n*2+2²-2² |
|
4²n²-2²= (*) |
|
| P=5 |
6²n²+30n= 36n²+30n+6-6 |
|
36n²-6n-6= 36n²-6n-6 |
|
| P=6 |
8²n²+48n= 8²n²+48n+8-8
|
|
8²n²-16n-8= 8²n²-2*8n+1-1 |
|
(*) si a+b = 0 alors on ne peut pas extrapoler ab
Exemple : quel est le triangulaire de 15 (P=3) ,c'est à dire juqsu'a quel nombre on ajoute pour obtenir 15 (1+2+3 ...?): 15*2=30 = 5*6 le plus petit facteur est un impair, jusque là rien d'extraordinaire puisque avec la formule x(x+1)/2 = T , x(x+1)=2T on arrive au même resultat
Autre exemple : cherchons maintenant la valeur du coté d'un pentagonal (P=5) = 145 (qui est égal au produit de 2 nombres/6) donc 6*145=6*5*29=29*30 , le plus petit terme étant impair alors il est issu de 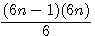 , donc 30=6*5 , donc 2n=10 !!!!
, donc 30=6*5 , donc 2n=10 !!!!
Notez que pour resoudre la problématique N°2 nous avons choisi la sequence (6n-1)(6n) parce qu'un des deux facteur est divisible par 6 ; en effet (6n+2)(6n+3) n'est pas divisible par 6.
Détails carrés pair
Décomposition de X² pair , obtention d'une représentation unique de x²
si x ![]() 0 (mod) 2 alors x = 2n <=> x = 2(n-1) +2 , faisons le carré:
0 (mod) 2 alors x = 2n <=> x = 2(n-1) +2 , faisons le carré:

factorisation de (n-1)

|
si x |
Je prouve par ce développement que le carré d'un nombre pair /4 est un autre carré en effet :
|
|
n² étant un carré pair ou impair alors si il est pair il suffit de le diviser de nouveau par 4 , si impair on lui retire 1...
Puisque le carré d'un nombre pair est un autre carré * 4 alors il suffit de divisé le carré jusqu'a l'obtention d'un carré impair , puis d'appliquer la méthode pour trouver la racine carré d'un nombre impair , par exemple:
 puisque nous avons divisé 2 fois par 4 alors
puisque nous avons divisé 2 fois par 4 alors 
nous avons donc décomposé 10.000 comme suit :  qui est égal à
qui est égal à 
Nous en déduisons donc la représentation universelle du carré d'un nombre
|
ou par factorisation :
|
![]() Pour la représentation d'un carré impair a=1 =>41(n)(n+1) + 40 = 4(n)(n+1)+1
Pour la représentation d'un carré impair a=1 =>41(n)(n+1) + 40 = 4(n)(n+1)+1
![]() Pour la représentation de 4a => n=0 , exemple 16 = 4² = 4²(0x1+1)=4²*1²
Pour la représentation de 4a => n=0 , exemple 16 = 4² = 4²(0x1+1)=4²*1²
Carrés pairs dans (a+b)²-(a-b)²=4ab
Carrés pairs dans (a+b)²-(a-b)²=4ab
|
Soit x² un carré , x²-y²+y²= x² <=> (x²-y²)+y²= x²
Hors dans l'équation (a+b)²-(a-b)² = 4ab on ne sait pas si :
Exemple a+b=10 ,a-b=4, (7+3)²/2² - (7-3)²/2² = (10/2)² - (4/2)² =5²-2²=7*3 Chaque terme de la soustraction est pair C.A.D (a+b) et (a-b)
Exemple (7+2)²-(7-2)²=9²-5²=56=4*7*2 c'est la différence de ces 2 carrés qui est divisible par 4 a est pair , b est impair ou vise-versa pour une somme a+b impair a est pair , b est impair ou vise-versa pour une diference a-b impair |
Rappel : L'équation de Diophante 4ab=(a+b)²-(a-b)²
Dans le livre 1 question xxx On donne la somme et le produit de deux nombres : trouver ces deux nombres. ,Diophante fait référence à l'équation:
C'est à dire : 4 fois le produit de 2 nombres = la somme de ces 2 nombres au carré - la difference de ces deux nombres au carré
Je détaille cette formule sur Youtubes https://youtu.be/givwc4Hftyc |
donc (x²-y²)+y²= x² , x est une somme impair de 2 nombres (a+b) , y sera = à (a-b) => x²= (a+b)²=4ab+(a-b)²
Dans l'équation 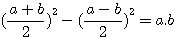 , => 4(a'+b')² - 4(a'-b')² = 4(a'+b')(a'-b') ou plus généralement 4n(a'+b')² - 4n(a'-b')² = 4n+1(a'+b')(a'-b')
, => 4(a'+b')² - 4(a'-b')² = 4(a'+b')(a'-b') ou plus généralement 4n(a'+b')² - 4n(a'-b')² = 4n+1(a'+b')(a'-b')
calculs annexes sur 4n+1
Cas 4n+1 , n est un carré donc 4n+1=> 4n' ² +1
Pour ce cas trouver les deux carrés qui composent un 4n+1 est facile:
Exemple 101 = 4(5²)+1 ; qui est égale à (2*5)(2*5) + 1² = 10²+1² , autre exemple 17 = 4*4+1 = 4²+1² , tout simplement parce que 4n² = (2n)(2n) +1 = (2n)²+1 . 2n = 2n
Autres cas :
Si un nombre à la forme 4n+1 ,premier ou non , égal donc à 2 * 2 * n + 1 , puisque 2xy+(x-y)² = x²+y² ; Si l'on remplace x par 2 , et y par n alors
|
|
Si n est premier c'est à dire = uniquement à n*1 , il n'y a que 2 solutions pour (n-2)² = 1 ...
Cas 4n+1 , n premier
Petite précision : tout nombre qu'il soit premier ou nom est égal à lui même * 1 C.A.D n=n+1 , seul les nombres premiers NE SONT = QU'A n x1
exemple 15 es tégal à 3x5 mais aussi 15x1 . Notez aussi que je prend n impair (de la forme 2n+1) parce que 2n n'est pas premier:
si (n-2)² = 1
Si un nombre à la forme 4n+1 et n x 1 , il est égal à 2 * 2 * n + 1 , donc il n'existe que 2 solutions pour que 4n+1 soit une hypothénuse:
|
Si n = 3 alors le 1 de 4(3)+1 sera égal à (3-2)² = 3² + 2² 13 = 4(3)+1 = 2*2*3+(3-2)² = 3²+2² |
Si n = 1 alors le 1 de 4(1)+1 sera égal à (1-2)² = 2² + 1² 5 = 4(1)+1= 2*2*1+(1-2)² = 1²+2² |
si (n-2)² <>1
|
Soit un nombre de la forme 4n+1 = donc a 2 x 2 x n + 1² alors il est "en réalité" =
correspondant à un "autre" 4(n+a) + 1 qui lui est une hypothénuse !!! exmple quelle sont les 2 carrés qui composent 4(13)+1 ? regardons le tableu dans la colonne "réel" nous pouvons voir qu'en fait 53 = 4(13)+1 = 2x2x7 + (7-2)² , puisque: 2xy+(x-y)² = x²+y² alors x=7 , y=2 : 53 = 7² + 2² |
en italique n n'est pas premier |
idem pour la "fameuse" hypothénuse = 29 = 4(7)+1 est en fait égal à 2x2x5 + (5-2)² = 5² + 2²
Mettons tout ça en équation : Si vous cherchez une équivalence avec 2xy+(x-y)² = x²+y² je vous promet de longues nuits blanches !!!!
L'astuce est en fait de remplacer N dans 4N+1 par 2n+1 (j'utilise N et 2n+1 au lieu de n et n' afin de rendre ce qui suit plus facile à lire)
Soit 4N+1 si N est impair remplaçons N par 2n+1, si N pair par 2*(2n+1)
|
remplacer N par 2n+1 |
remplacer N par 2n+1 |
|
|
|
|
Donc : si un (4N+1 -5) /4 est un produit de forme n(n+1) alors Z² = (2n+1)²+2²Exemple 4(7)+1 = 29 - 5 = 24 / 4 = 6 , 6 = 2*3 , "2n+1" =>n = 2 donc 29 = 5² +2²
|
Donc : si un (4N+1 -17) /4 est un produit de forme n(n+1) alors Z² = (2n+1)²+4²Exemple 4(10)+1 = 41-17 = 24/4 = 6=2*3 , "2n+1" =>n = 2 donc 41 = 5² +4² |
Cas N non premier , N=xy/2
|
Si N est un produit d'au moins deux nombres x*y /2 ; tel que: Pour 4N+1 = 2*2*(xy/2)+(2x-y)² =2xy+(2x-y)² , si 2x-y = 1 ou - 1 alors trouver les 2 carrés que composent 4n+1 devient aussi extrémement facile. Autrement dit , dans le cas ou n est un nombre Triangulaire ! |
rappel: (n+1)-(n) = 1 , n+n+1 = 2n+1 , 2(n)(n+1)/2 = n(n+1) |
Exemple : 41 = 4(10)+1 =>10=(4*5)/2 = 2[2*2*5]+1 = 2x=4 , y=5 donc 2*4*5 + (4-5 = -1)² = 4²+5² , 16+25 est bien égal à 41.
Autre exemple : Trouvez les carrés que composent 61 , solution : 61 = 4(15)+1 = 2 * 5 * 6 +(6-5)²= 5²+6² (25+36 = 61)
Citations
La solution de Fermat
Quels sont mes pistes : Dans le Livre III question 22 (L3Q22) Trouver 3 nombres tels , que le carré de leur somme étant soustrait de chacun d'eux , les restes soient des carrés
OBS DE FERMAT. Un nombre premier qui surpasse de 1 tout multiple de 4 , est une seule fois l'hypoténuse d'un triangle rectangle (formé de cotè entiers), ....
Dans le Livre V question 12 (L5Q12) Diviser l'unité en deux parties telles que la somme de chaque partie et d'un nombre donné soit un carré.
OBS DE FERMAT. Cette limitation est vraie et générale , puisqu'elle exclut tous les nombres inutiles ; il faut que le nombre donné ne soit pas impair et que le quotient de son double , augmenté d'une unité par le plus grand carré qui le mesure , ne puisse être divisé par aucun nombre premier égal à un multiple de 4 diminué de 1.

Patrick Stoltz le 22/09/2017
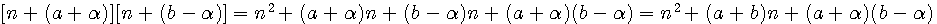

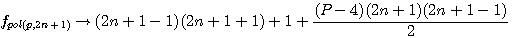
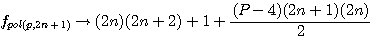
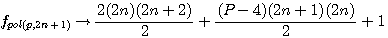
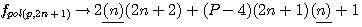
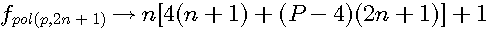
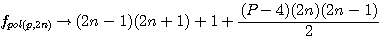
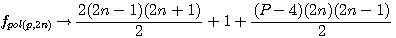
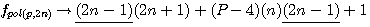
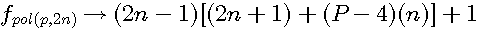
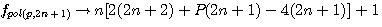
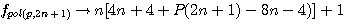
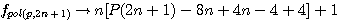
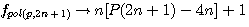
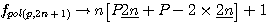
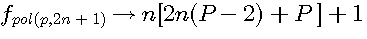
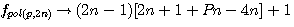
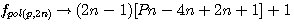
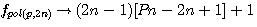
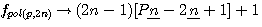
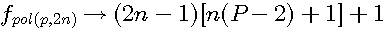
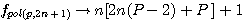
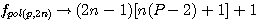
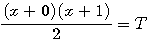 ;
; 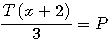 :
: 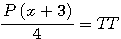 et la formule générale expression confirmée par la lettre de Pierre de Fermat à Roberval du 4 Novembre 1636 ou l'on trouve l'expression suivante
et la formule générale expression confirmée par la lettre de Pierre de Fermat à Roberval du 4 Novembre 1636 ou l'on trouve l'expression suivante 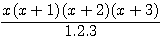 ....
....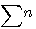 )
)
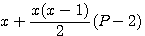
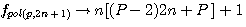 =
=