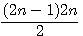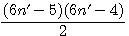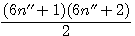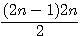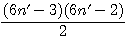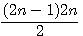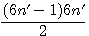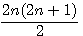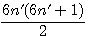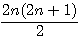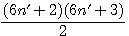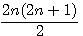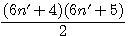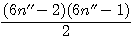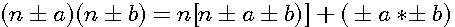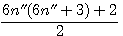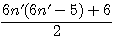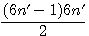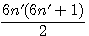|
Synthése des études de Pierre de Fermat
Contexte :
L'arithmetica de Diophante (environ 200-300) est une liste de questions arithmétiques contenues dans VI livres . Par la suite,l' arithmetica fut étudié et annoté par Bachet (1581-1638) , par Fermat(1601-1665) et en 1853 par Emile Brassine (*), professeur à l'école impériale d'artillerie de Toulouse.
C'est au cours de l'étude du livre II question 9 de l'Arithmetica de Diophante que Fermat a posé son grand théorème ( 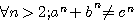 ) ; Il est dit que Fermat ne disposait pas d'outils mathématiques suffisant pour énoncer son Grand théorème, tout au plus pour n3 ou n4 .Il fut démontré 300 ans plus tard par Andrew Wiles (Un document de plus de 120 pages que seul un vingtaine de mathématiciens peuvent comprendre )
) ; Il est dit que Fermat ne disposait pas d'outils mathématiques suffisant pour énoncer son Grand théorème, tout au plus pour n3 ou n4 .Il fut démontré 300 ans plus tard par Andrew Wiles (Un document de plus de 120 pages que seul un vingtaine de mathématiciens peuvent comprendre )
Il n'y a pas que le grand théorème qui ne fut pas démontré par Pierre de Fermat mais aussi :
![]() Son théorème des hypothénuse 4n+1 (4n+1 est la somme de 2 carrés)
Son théorème des hypothénuse 4n+1 (4n+1 est la somme de 2 carrés)
|
|
n Si vous n'êtes pas familier avec la notation de l'arithmétique modulaire cliquez sur ce lien pour un petit rappel |
![]() Dans la question 31 du livre IV Fermat fait l'observation suivante: Que tout nombre est triangulaire ou composé de deux ou de trois triangulaires; carré ou composé de deux , de trois ou de quatre carrés ; pentagones ou composé de deux , trois , quatre ou cinq pentagones, et ainsi de suite à l'infini... théorème non démontré par Fermat et pour lequel
il voulait écrire un livre ...
Dans la question 31 du livre IV Fermat fait l'observation suivante: Que tout nombre est triangulaire ou composé de deux ou de trois triangulaires; carré ou composé de deux , de trois ou de quatre carrés ; pentagones ou composé de deux , trois , quatre ou cinq pentagones, et ainsi de suite à l'infini... théorème non démontré par Fermat et pour lequel
il voulait écrire un livre ...
Et puis il y eut la lettre du 4 Novembre 1636 de Fermat à Roberval où l'on retrouve l'expression suivante: 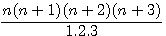 ...
...
Ma démarche :
J'ai toujours pensé que Pierre de Fermat n'était pas un menteur , mais qu'il avait posé ces théorèmes , à tord ou à raison , grâce à une ou plusieurs formules clef suffisamment simple pour être mémorisées , car Fermat , magistrat de métier , devait avoir ces formules clef en tête pour ses études , et que celles-ci étaient passées inaperçu au cour des siècles.
J'ai donc entrepris , pendant 12 ans , d'étudier un bon nombre de ses annotations sur l'arithmetica de Diophante, de les traduire par des formules mathématiques littérales , et de les publier (Page arithmetica de ce site) , afin de trouver ces clefs eu où il avait eût ce déclic ...
Je me suis vite aperçu que Fermat avait évoqué son grand théorème au début de l'Arithmetica (Livre II), mais que ce déclic a eut lieu sur la fin (Livre IV question 31).
Vous constaterez par la suite que Fermat , dans toutes ses thèories , exploitait un nombre x composé d'une partie multiple de n et une autre pas , (par exemple 4n+1) ce qui est le principe même des nombres complexes . (exemple 4i+1...)
Introduction à la clef de Fermat
Observation de Fermat sur l'étude du problème de Diophante (Livre sur les nombres polygonaux question 4): Etant donné un nombre polygonal trouver le coté
Qu'est ce qu'un coté d'un polygone ?
Nous avons trouvé une belle et admirable proposition que nous placerons ici sans démonstration.
Dans la progression des nombres naturels commençant par l'unité, un nombre quelconque, multiplié par celui qui le suit et qui est plus grand, fait le double du triangulaire de ce nombre;
La multiplication du triangulaire, par le nombre qui le suit et qui est plus grand dans la progression, donne le triple du pyramidal;
Le produit du pyramidal, par le nombre suivant de la progression, donne le quadruple du triangulo--triangulaire, et ainsi à l'infini par une méthode générale et uniforme;
J'avais , dans un premier temps, traduit à tort par 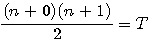 ;
; 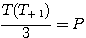 ;
;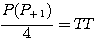 et rectifié en 2015 par
et rectifié en 2015 par
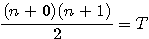 ;
; 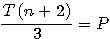 :
: 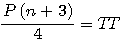 mais j'avais bien traduit par l'expression suivante :
mais j'avais bien traduit par l'expression suivante :
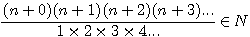
expression confirmée par la lettre de Pierre de Fermat à Roberval du 4 Novembre 1636 ou l'on trouve l'expression suivante:
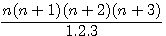 .
.
et je ne pense pas qu'on puisse donner sur les nombres un théorème plus beau et plus général, je n'ai ni le loisir ni la convenance d'insérer la demonstration à la marge
Matrice des "cotés" de nombres polygonaux
|
1! |
2! ( |
3! (P) |
4!(TT) |
5! |
6! |
7! |
|
n /1 |
n(n+1) /2 |
n(n+1)(n+2) /6 |
n(n+1)...(n+3) /24 |
n...(n+4) /120 |
n...(n+5) /720 |
n...(n+6) /5040 |
| N=1 |
1 |
1 |
1 |
1 |
1 |
1 |
| N=2 |
3 |
4 |
5 |
6 |
7 |
8 |
| N=3 |
6 |
10 |
15 |
21 |
28 |
36 |
| ...4 |
10 |
20 |
35 |
56 |
84 |
120 |
| 5 |
15 |
35 |
70 |
126 |
210 |
330 |
| 6 |
21 |
56 |
126 |
252 |
462 |
792 |
| 7 |
28 |
84 |
210 |
462 |
924 |
1716 |
| 8 |
36 |
120 |
330 |
792 |
1716 |
3432 |
| 9 |
45 |
165 |
495 |
1287 |
3003 |
6435 |
| 10 |
55 |
220 |
715 |
2002 |
5005 |
11440 |
| 11 |
66 |
286 |
1001 |
3003 |
8008 |
19448 |
| 12 |
78 |
364 |
1365 |
4368 |
12376 |
31824 |
| 13 |
91 |
455 |
1820 |
6188 |
18564 |
50388 |
| 14 |
105 |
560 |
2380 |
8568 |
27132 |
77520 |
| 15 |
120 |
680 |
3060 |
11628 |
38760 |
116280 |
| 16 |
136 |
816 |
3876 |
15504 |
54264 |
170544 |
| 17 |
153 |
969 |
4845 |
20349 |
74613 |
245157 |
| 18 |
171 |
1140 |
5985 |
26334 |
100947 |
346104 |
| 19 |
190 |
1330 |
7315 |
33649 |
134596 |
480700 |
| 20 |
210 |
1540 |
8855 |
42504 |
177100 |
657800 |
| 21 |
231 |
1771 |
10626 |
53130 |
230230 |
888030 |
| 22 |
253 |
2024 |
12650 |
65780 |
296010 |
1184040 |
2! signifie factorielle de 2 C.A.D 2! = 1x2 ; 5! = 1x2x3x4x5
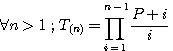 = la colonne
= la colonne 
Colonne T = 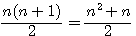 = Ligne N=3 si N >2
= Ligne N=3 si N >2
Colonne P = 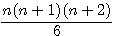 = Ligne N=4 si N > 3
= Ligne N=4 si N > 3
Colonne TT = 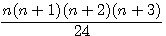 = Ligne N=5 si N > 4
= Ligne N=5 si N > 4
J'avais (en 2010) relevé l'importance de cette formule , Pierre de Fermat ayant terminé cette observation par "je n'ai ni le loisir ni la convenance d'insérer la demonstration à la marge" , même phrase qu'il utilise à la fin de son grand théorème; Même si cette matrice ressemble à un triangle de Pascal , et a un certain nombre de propriétés intéressantes , je n'avais pas compris son intérêt au point d'être "sur les nombres un théorème plus beau et plus général"
Jusqu'a ce que je tente de résoudre (en 2015),sans calculatrice et sans à avoir à résoudre une équation du second degrés, l'expression d'un nombre triangulaire : soit 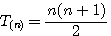 trouver n
trouver n
En résumé (Détails sur ce lien) , si nous observons bien cette matrice alors nous constatons que la colonne 2!  est égale à la ligne n=3 à partir de
est égale à la ligne n=3 à partir de  (3)
(3)
Ce qui implique que si un nombre est un Triangulaire T(n) alors , dans la formule 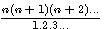 , il nous suffit de remplacer n par 3 , (nombre de cotés d'un triangle) pour égaler le nombre de facteurs du numérateur et du diviseur . Pour compter le nombre de facteurs du numérateur l'on compte de 1 à (n+1) ou du diviseur on compte de 1 à (n-1) => 3*4*....(n+1) / 1*2*3*(n-1)
, il nous suffit de remplacer n par 3 , (nombre de cotés d'un triangle) pour égaler le nombre de facteurs du numérateur et du diviseur . Pour compter le nombre de facteurs du numérateur l'on compte de 1 à (n+1) ou du diviseur on compte de 1 à (n-1) => 3*4*....(n+1) / 1*2*3*(n-1)
Exemple si  (5) = 15 alors
(5) = 15 alors 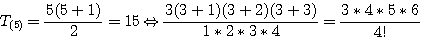
pour  (5), comptons 3,4,5,6 c'est à dire 4 facteurs 5-1 facteurs , le premier facteur = 3 le dernier facteur = n+1 ; La valeur du coté d'un triangulaire de valeur 15 est 5 c'est a dire 3*4*5*6 = 360 / 24 = 15 , mais c'est aussi (6!/2)/4!
(5), comptons 3,4,5,6 c'est à dire 4 facteurs 5-1 facteurs , le premier facteur = 3 le dernier facteur = n+1 ; La valeur du coté d'un triangulaire de valeur 15 est 5 c'est a dire 3*4*5*6 = 360 / 24 = 15 , mais c'est aussi (6!/2)/4!
J'en ai donc déduit que :
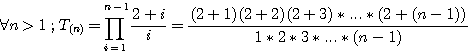
Très important : le dernier facteur = (2+(n-1)) = (n+1)... (le dernier facteur du numérateur (n+1) multiplié par l'inverse du dernier facteur du diviseur (inverse de 1/(n-1)=(n-1)) est = n²-1
Exemple ci dessus : pour T(5) alors 6*4 = 5²-1
et puisqu'un triangulaire égale la somme des nombres de 1 à n alors:
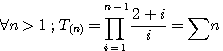
Suite des applications de cette formule au paragraphe de cette page Arithmética Livre IV Question 31
0!
Dans ces égalités colonnes / lignes, examinons la colonne 1! = N/1 et la ligne N=2.
Pour n>1 , La colonne 1! égale la ligne N=2.
Exemple : 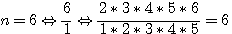 ; nombre de facteurs n-1 = 5 , le numérateur = 2x3x4...n, le dénominateur = 1x2x3 ... (n-1)
; nombre de facteurs n-1 = 5 , le numérateur = 2x3x4...n, le dénominateur = 1x2x3 ... (n-1)
Encore rien d'extraordinaire mais nous comprenons déjà pourquoi le nombre 1 est exclus de cet ensemble car si nous incluons 1 dans cet exemple alors 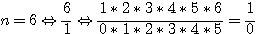 est donc ne serait plus vrai. (ce qui produit dans les factorielle la problématique de la convention 0!=1 dont nous nous passerons)
est donc ne serait plus vrai. (ce qui produit dans les factorielle la problématique de la convention 0!=1 dont nous nous passerons)
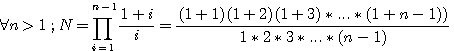
nota : Le dernier facteur du numérateur, (1+n-1) = n
n=3 ...
Pierre de Fermat au (suget des hypothénuses 4n+1) écrit en marge dans le livre V question 12 :
OBS. DE FERMAT: Le nombre 21 ne peut pas être divisé en fraction en deux carrés, nous pouvons facilement démontrer cela , et plus généralement, que tout nombre dont le tiers n'est pas lui même divisible par trois, ne peut être décomposé en deux carrés , ni entiers ni fractionnaires.
A force d'essayer de comprendre la relation de cette phrase avec toutes les autres annotations (sus et sous nommées) de Pierre de Fermat , j'en conclus que Pierre de Fermat avait trouvé cette relation FONDAMENTALE sur les nombres (déjà entrevue ci-dessus ):
|
il existe un seul et unique nombre n tel que le produit de 1 à n = la somme de 1 à n |
Autrement dit :seulement 1*2*3 = 1+2+3 |
Seulement la somme de trois nombre consécutifs (de 1 à 3) égale le produit de ces trois nombres consécutifs
nota : Vous pouvez m'objecter que 1 = 1*1 mais 1 n'est pas une somme , 1 est égal à la somme de 0 + 1 <> 1*0 ou 1/2+1/2 <> 1/2*1/2
| 1*1 | 1*2 | 1*2*3 | 1*2*3*4 | 1*2*3*4*5 | |
| 1+1 | 2>1 | ||||
| 1+2 | 3>2 | ||||
| 1+2+3 | 6=6 | ||||
| 1+2+3+4 | 10<24 | ||||
| 1+2+3+4+5 | 15<120 |
Pourquoi la pièce est noire ?
Cette égalité ,qui parait anodine, à de très nombreuses applications .Elle établi une relation entre la logique (binaire) et les nombres : Si vous entrez dans une pièce plongée dans le noir, est elle noire par ce que la lumière est éteinte (photons) ou par ce qu'il n'y a pas d'ampoule (matière)? Pourquoi ,la nuit, ciel est noir ? par ce qu'il n'y a pas de lumière ou par de masse ? Nous verrons que ce système logique établi une PRIORITE dans cette relation , c'est à dire que pour avoir de la lumière il faut d'abord remplacer l'ampoule pour avoir de la lumière . ou , pour avoir un oeuf, il faut d'abord avoir une poule (ce qui implique que la poule est venu avant l'oeuf !!!)
Nous savons que l'arithmétique binaire (allumé ou éteint ) à besoin du complement à deux pour traiter le zéro et les nombres négatifs et qu'en fait il existe deux zéros.... Ce système "obeit" en fait au système (trinaire) suivant : (n-1)(n)(n+1) relatif à la factorielle de trois nombres consécutifs.
![]() Nous remarquons aussi que :
Nous remarquons aussi que :
|
|
et aussi |
|
![]() J'avais aussi remarqué la relation entre les nombre premier et 6 au sujet des nombres triangulaires
J'avais aussi remarqué la relation entre les nombre premier et 6 au sujet des nombres triangulaires
![]() Décomposition des nombres :
Décomposition des nombres : 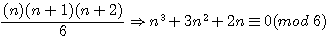 et si n n'est pas un multiple de 3
et si n n'est pas un multiple de 3
|
si n
|
Clef de Fermat N°1 : Vision "bi-triangulaire" d'un nombre pair ->2n , impair 2n+1
Orientation de mes recherches:
OBS DE FERMAT. Un nombre premier qui surpasse de 1 tout multiple de 4 , est une seule fois l'hypoténuse d'un triangle rectangle (formé de cotè entiers), son carré deux fois, son cube trois fois , sa quatrième puissance quatre fois, etc à l'infini.
Dans le Livre V question 12 (L5Q12),
OBS DE FERMAT. Cette limitation est vraie et générale , puisqu'elle exclut tous les nombres inutiles ; il faut que le nombre donné ne soit pas impair et que le quotient de son double , augmenté d'une unité par le plus grand carré qui le mesure , ne puisse être divisé par aucun nombre premier égal à un multiple de 4 diminué de 1.
J'en ai donc déduit que Fermat se représentant une hypothénuse première ayant la forme 4n+1 alors il a donc representé un nombre pair comme ayant une "forme" 2n et un nombre impair ayant la forme 2n+1...
nombre pair =2n , nombre impair = 2n+1
Soit un nombre x , si ce nombre est > à 1 alors il est composé d'au moins de la somme de deux nombres que nous appellerons n et b.par exemple 13 est = à 1+12 , 2+11 , 3+10 etc.... (et aussi le produit d'au moins deux nombre même si il est premier par exemple 13 = 13*1)
Ce nombre peut aussi être maintenant décomposé en n le premier terme et b le deuxième terme égal à n + ![]() ,
, ![]() étant la différence de b et n . Exemple 13 = 5+8 , 13 = 5 + 5+3. si l'on factorise le premier terme de l'addition alors x = 2n +
étant la différence de b et n . Exemple 13 = 5+8 , 13 = 5 + 5+3. si l'on factorise le premier terme de l'addition alors x = 2n + ![]() , 13 = 2(5) +3
, 13 = 2(5) +3
|
|
Ce nombre peut aussi être décompose en n = b , et - ![]() , par exemple 13 = 8 + 8 - 3 ,c'est a dire 13 = 2(8)-3
, par exemple 13 = 8 + 8 - 3 ,c'est a dire 13 = 2(8)-3
|
|
Si le nombre x est impair alors nous pouvons remplacer ![]() par 1 et n devient unique ; c'est a dire 13 = 2(6)+1
par 1 et n devient unique ; c'est a dire 13 = 2(6)+1
Si le nombre x est pair alors nous pouvons remplacer ![]() par 0 et n devient unique ; c'est a dire 12 = 2(6)+0
par 0 et n devient unique ; c'est a dire 12 = 2(6)+0
|
si x si x |
Nous pouvons écrire aussi que :
|
si x premier alors Exemple 17=4+12+1=>17=2(2+6)+1=2(2+2*3)+1 |
Trouver le carré d'un nombre
Grâce à cette formule nous pouvons donner une image au carré d'un nombre , si x = 2n + ![]() alors x² = (2n +
alors x² = (2n + ![]() )²
)²
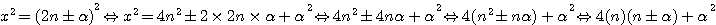
exemple 13 = 2*5 + 3 , alors 13² = 4*5*(5+3)+3² <=> 20*8 + 9 <*=> 160+9 *= 169
|
|
|
Et donc ,pour un nombre impair, si je remplace
rappel : n(n+1) est un nombre oblong ,il est égal à deux fois un nombre triangulaire Si je reprend l'exemple ci dessus alors 13 = 2*6 + 1 , son carré 132 est égal à 4(6)(7)+1 = 4*42 +1 = 168 +1 = 169 Pour élever un nombre impair au carré il suffit de prendre (X -1) / 2 =n , pour trouver le premier facteur n de (n)(n+1) , puis multiplier (n)(n+1) par 4 et lui ajouter 1 pour obtenir son carré Exemple 13² = (13-1)/2 = 6 => 6x7 = 42 x 4 = 168 +1 = 169 le carré de 13 Autre exemple 15² = (15-1)/2 = 7 => 7 x 8 =56 x 4 = 224 +1 = 225 |
Et donc ,pour un nombre pair, si je remplace
Exemple 6² = (2*3)² = 2² x [2²(1)(*2)+1] = 4 x [4(1)(2)+1] = 4 x (8+1) = 36 . |
|
Remplacer x par n = démonstration x²= 4(n)(n+1) +1 ou 4n² si dans x=2n+1 nous remplaçons x par n alors TOUT nombre n peut être exprimé sous la forme : n² = ?
si l'on factorize par 4 (n-1)/2 les deux premiers termes :
|
Playlist you_tubes sur les clefs de Fermat |
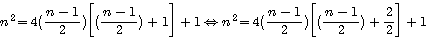 <=>
<=> 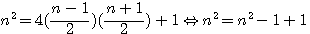
l'on peut en déduire que pour trouver le carré d'un nombre n l'on peut appliquer (n-1)(n+1)+1 ; 13² = 12/2*14/2+1 => 6*7+1 mais le plus important étant: (n-1)/2+(n+1)/2=n la somme des deux facteurs de (n-1)(n+1)/4+1 , mais aussi (n-1)(n+1)+1 => (n-1)+(n+1)+1=2n+1
Carré d'un nombre et factorielle :
Reprenons le numérateur de l'expression 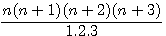 . (que l'on trouve dans la lettre de Pierre de Fermat à Roberval du 4 Novembre 1636 ) , nous remarquons donc qu'un facteur est = au facteur précédent multiplié par le facteur suivant +1 , par exemple pour (n+2)² , le facteur précedent = (n+1) le suivant (n+3) donc (2n+2)²=(n+1)(n+3)+1 . Autre exemple (n+1)² = n(n+2)+1
. (que l'on trouve dans la lettre de Pierre de Fermat à Roberval du 4 Novembre 1636 ) , nous remarquons donc qu'un facteur est = au facteur précédent multiplié par le facteur suivant +1 , par exemple pour (n+2)² , le facteur précedent = (n+1) le suivant (n+3) donc (2n+2)²=(n+1)(n+3)+1 . Autre exemple (n+1)² = n(n+2)+1
CF2 : Trouver la racine carré entière d'un nombre 2n ou 2n+1
Racine carrée d'un nombre pair 2n:
Si n est pair alors 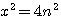 c'est a dire 4 fois n*n (2²n*n) , si l'on ajoute les deux facteurs alors n² => n+n
c'est a dire 4 fois n*n (2²n*n) , si l'on ajoute les deux facteurs alors n² => n+n
Exemple : Trouvons la racine carrée de 144 , 144/4 = 36 = 6*6 => 6+6 = 12
|
si x si
|
si le n de 4n² est aussi un carré divisile par 4 alors 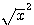 = 2*2(n) et ansi de suite jusqu'à l'obtention d'un carré impair pour
= 2*2(n) et ansi de suite jusqu'à l'obtention d'un carré impair pour 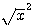 entiére .
entiére .
Meme pour racine de 4 = 2 = 2*1 , 1 est impair
Trouvons la racine carrée de 144 , 144/4 = 36 , 36/4 = 9 racine de 9 = 3 donc racine carré de 144 = 2*2*3 = 12
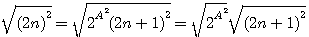
En résumé : si un nombre à la forme 2n alors il à la forme 2a(2n+1)
Racine carrée d'un nombre impair
Ce théorème est basé sur les travaux sur les nombre polygonaux de Pierre de Fermat.
|
Racine carrée d'un nombre impair: Soit x un nombre impair donc de la forme 2n + 1 ,son carré égal si l'on ajoute les deux facteurs de
|
|
si x
somme des facteurs de :
|
Exemple: Trouvons la racine carrée de 289 , 289 -1 = 288 divisé par 4 = 72 = 2*36 = 4*18 = 8*9 => 8+9 = 17 ;
(2n+1 = 17 , n est égal à 8) ; la valeur de n a pas d'importance(pour le moment) , c'est 2n+1 qui est la racine de x² =(2n+1)²
Si n(n+1) est le produit de plus de 2 nombres (a*b*c*d) , il suffit donc de décomposer n(n+1) en ses plusieurs facteurs , la somme de ces facteurs -1 sera égale à n. c'est à dire (a+b-1) = (c+d) ou (a+c)-1 = (b+d) .....
Pourquoi le nombre d'or ?
Le fait de transformer (n)(n+1) en 2n+1 pour trouver la racine d'un carré, c.a.d faire la somme des facteurs de (n) et (n+1) , se résume à poser:
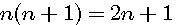
C.a.d : Faire la somme d'un produit de 2 nombres consécutifs
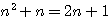
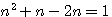
Soit la définition du nombre d'or :
|
<=>
<=>
|
plus de détails sur le nombre d'or sur:
Clef de fermat N°3 Equation du second degrés
|
En prolongement des chapitres precedents nous nous apercevons que la progression (n)(n+1).... et le nombre d'or ne sont que des équations du second degrés simplifiée. sur cette page , je démontre une équation du second degrés selon une équation diophantesque n(n+1) ... |
Clef de fermat N°4 : les Poly polygonaux
Sur l'étude du livre "les nombres polygonaux" de Diophante ( question : Etant donné un nombre polygonal trouver le coté ) Fermat expose le théorème suivant :
Nous avons trouvé une belle et admirable proposition que nous placerons ici sans démonstration.
Dans la progression des nombres naturels commençant par l'unité, un nombre quelconque, multiplié par celui qui le suit et qui est plus grand, fait le double du triangulaire de ce nombre;
La multiplication du triangulaire, par le nombre qui le suit et qui est plus grand dans la progression, donne le triple du pyramidal;
Le produit du pyramidal, par le nombre suivant de la progression, donne le quadruple du triangulo--triangulaire, et ainsi à l'infini par une méthode générale et uniforme; et je ne pense pas qu'on puisse donner sur les nombres un théorème plus beau et plus général, je n'ai ni le loisir ni la convenance d'insérer la demonstration à la marge (1)
Ce que je traduit par : 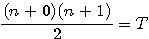 ;
; 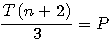 :
: 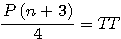
Qui par déduction donne l'expression suivante : 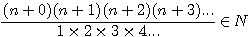
Clef de fermat N°5 : Démonstration du petit Théorème de Fermat
Soit la formule 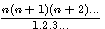 et que nous développons le numérateur alors nous obtenons un expression du genre :
et que nous développons le numérateur alors nous obtenons un expression du genre :
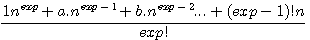 ,
,
par exemple pour 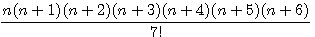 =
= 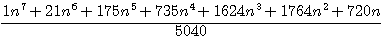
|
Si l'on considère que Fermat a développé toutes ses théories (petit et grand théorème) pour toutes les puissances de n, il est bien sur totalement exclus , pour trouver tous les indices (exemple ci-dessus 1,21,175,735,1634,1764,720), que Fermat ait procéder un calcul manuel.
Comment trouver la somme des indices? si dans la formule : |
|
Si nous développons le numérateur alors la somme des termes de l'addition ainsi obtenue sera égale à la factorielle du nombre de facteurs du dénominateur.
Exemple :
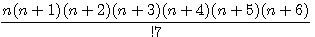 <=>
<=> 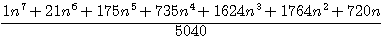 et remplaçons n par 1 (ligne en bleue sur le tableau ci-dessus) alors :
et remplaçons n par 1 (ligne en bleue sur le tableau ci-dessus) alors :
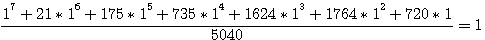 , 1+21+175+735+1624+1764+720=5040 = 7!
, 1+21+175+735+1624+1764+720=5040 = 7!
![]() Dans une équation de la forme n(n+1)(n+2)... la somme des indices égale à la factorielle du nombre des facteur de cet équation
Dans une équation de la forme n(n+1)(n+2)... la somme des indices égale à la factorielle du nombre des facteur de cet équation
![]() Le premier exposant = le nombre de facteurs (comme pour un tableau de Pascal), dans l'exemple 17.
Le premier exposant = le nombre de facteurs (comme pour un tableau de Pascal), dans l'exemple 17.
![]() Le dernier indice = factorielle -1 du nombre de facteurs.
Le dernier indice = factorielle -1 du nombre de facteurs.
Rappel de la définition:
|
Soit n un nombre entier > 1 et p un nombre entier premier alors |
n Si vous n'êtes pas familier avec la notation de l'arithmétique modulaire cliquez sur ce lien pour un petit rappel |
Exemple : si n=10 et p = 5 alors 105-10 0 (mod 5 ) , 100000-10 = 99990 est divisible par 5
Dans cette définition 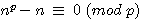 est aussi
est aussi 0 (mod n )
suite sur :
Loi sur la décomposition d'un produit de deux nombres
Nous avons exploité au chapitre précédent une expression du type (n)(n+1)(n+2)(n+3)..... avec des indices multiples de n et d'autre non.
|
Si dans cette expression nous prenons 2 facteurs quelquonque, par exemple (n+1) et (n+5) alors (n+1)(n+5) = n² + 1n + 5n + 1*5 = n² + 6n + 5 = n(n+6)+5 Si nous généralisons cet exemple alors: :
Exemple 3 * 7 = 21 = (2+1)(2+5) = 2(2+6)+5 = 2*8+5 =16+5= 21 |
factorisation de n
donc
|
Cette même loi est applicable pour + et pour -
|
<=>
|
Exemple 3*7 = 21 = (4-1)(4+3) = 4(4+2)-3 = 24-3
Clef_7 Soit un nombre premier de forme 4n+1 , trouver les 2 carrés qui le composent
J'ai entrepris depuis de nombreuses années d'étudier et de détailler toutes les notes de Pierre de Fermat sur l'Arithmética ; Il s'avère que ses annotations les plus récurrentes ne sont pas , comme on pourrait s'y attendre , son petit Théorème, les nombres polygonaux, ou les triangles de Pascal mais sont relatives à son théorème dit : "des deux carrés".
Ce théorème est cité entre autre dans le Livre III question 22 (L3Q22) en ces termes :
OBS DE FERMAT. Un nombre premier qui surpasse de 1 tout multiple de 4 , est une seule fois l'hypoténuse d'un triangle rectangle (formé de cotè entiers), son carré deux fois, son cube trois fois , sa quatrième puissance quatre fois, etc à l'infini.
Dans cette questrion Fermat divise une hypothénuse par des 4n+1 et "range" les exposants afin de compter combien de fois un 4n+1 est une hypothénuse.
On remarque qu'une hypothénuse premiére de la forme 4n+1 EST elle même COMPOSEE de deux carrés ( si k=1 alors 4n +1 = 1²(x'² + y'²) )
Par exemple 5²+12²=13² , 13 étant de forme 4n+1 , alors il est lui même composé de 2 carrés 2²+3²=13
J'en ai conclus que Fermat avec son théoréme des hypothénuses 4n+1, s'est représenté une autre image d'une hypothénuse , autre que la formule
(x²-y²)²+(2xy)² = (x²+y²)² .et aprés 10 ans de recherches je démontre que tout nombre premier de la forme 4n+1 est composé de 2 carrés.
x²+y²=2xy+(x-y)²
Soit (x-y)² = x²-2xy+y² alors (x-y)²+2xy = x²-2xy+y²+2xy = x²+y² les 2 carrés de base de la formule (x²-y²)²+(2xy)² = (x²+y²)²
Z = x²+y² = 2xy+(x-y)²pour x<>y |
On note que si Z est la somme de 2 carrés de base alors Z-la difference de x et y au carré = 2 fois le produit x et y.exemple : 61 -1² = 2*6*5 ; 61=6²+5² autre exemple 29-3²=2*5*2 = 5²+2²
Z = x²+y² - 2xy = (x-y)² |
Cette formule fonctionne aussi pour Z non premier et aussi pour x-y pair
![]()
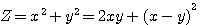 + 2xy = (x+y)² CAD : 4xy + (x-y)²= (x+y)²
+ 2xy = (x+y)² CAD : 4xy + (x-y)²= (x+y)²
Z+2xy = 4xy + (x-y)² = (x+y)²si (x+y)² est non premier alors : k²(4xy + (x-y)²) = k²(x+y)²si (x+y)² est premier alors : 1²(4xy + (x-y)²) = 1²(x+y)² |
La difficulté pour Z = x²+y² = 2xy+(x-y)² est de trouver l'écart x-y pour le nombre donné pour peu que celui ci soit une hypothénuse !!!
Par exemple 21-1² =20/2 = 2*5 l'écart entre 2 et 5 est 3 différent de 1 . 21 n'est pas une hypothénuse.
Si N= Z ,Z=2xy+(x-y)² , si (x-y)² = 1 celà est assez facile , par exemple 41-1 = 40/2 =20 = 4*5 , 41 = 4²+5² , si cet ecart est autre celà devient plus difficile, par exemple 101 => 2*10*1 + 81 = 10²+1²
en résumé :
Z = x²+y² = 2xy+(x-y)²(x+y)² = 4xy+(x-y)² |
Z =4n+1 non premier
Dans le Livre V question 12 (L5Q12),
OBS DE FERMAT. Cette limitation est vraie et générale , puisqu'elle exclut tous les nombres inutiles ; il faut que le nombre donné ne soit pas impair et que le quotient de son double , augmenté d'une unité par le plus grand carré qui le mesure , ne puisse être divisé par aucun nombre premier égal à un multiple de 4 diminué de 1.
Emile Brassine ajoute : D'après Fermat si x et y ne sont pas premier entre eux et qu'ils aient un facteur commun k, on aura 4n +1 = k²(x'² + y'²), par la suite (4n+1)/k² = x'² + y'² ; or le quotient du premier membre étant la somme de deux carrés , ne saurait être divisé par aucun nombre premier de la forme 4n-1, ce qui est encore un théorème de Fermat.
Si pour p>3 , p²-1 est divisible par 24 alors à quoi est congru a² + b² premier ?
Soit z=4n+1 une hypothénuse premiére alors 4n ou 4n-1 est divisible par 3 .En effet si z² = (a²+b²)² alors (4n + 1)² = (4n+1-1)(4n+1+1) + 1 = (4n)(4n+2) +1. Si 4n+2 0 mod 3
alors 4n+2 - 3 = 4n-1 est aussi 0 mod 3 (rappel n
0 mod 3 signifie n est divisible par 3 , le reste =0)
|
4n |
4n-1 |
||
|
si 4n
factorisation par n/3
on note que 3² + 3 = 12 = 1*2*3*4 / 2 = 4!/2
exemple 4(9)+1 = 37 = (1*2*3*4*9)/6 +1 |
si 4n-1
puis que (n-1)
Il y a un moyen plus rapide de prouver cette équation , mais le + 5 a une énorme importance,
|
Clef N°8 Arithmética Livre IV Question 31 Théorème fondamental de Fermat sur les nombres polygonaux
Dans la question 31 du livre IV Fermat fait l'observation suivante:
OBS DE FERMAT. Bien plus , j'ai découvert le premier une proposition très belle et très générale, savoir ; que tout nombre est triangulaire ou composé de deux ou de trois triangulaires; carré ou composé de deux , de trois ou de quatre carrés ; pentagones ou composé de deux , trois , quatre ou cinq pentagones, et ainsi de suite à l'infini, on peut énoncer cette merveilleuse proposition pour les hexagones , les heptagones , et généralement pour les polygones quelconques, d'après le nombre de leurs angles. Mais il ne convient pas de placer ici sa démonstration qui est déduite de plusieurs mystères les plus variés et les plus abstrus des nombres , car nous avons résolu de destiner à cet objet un Livre complet, et d'étendre merveilleusement dans cette partie l'arithmétique au delà de ses anciennes limites connues.
Fermat n'a jamais écris ce livre et aujourd'hui encore on (source wikipédia) lui reproche de ne pas avoir démontrer ce théorème ..... mais il est suffisamment important pour Fermat pour qu'il envisage d'écrire un livre !..
L'histoire n'a retenue que la décomposition d'un nombre en 1,2,3 ou 4 carré ,mais ,en fait, un carré n'est qu'un cas particulier (somme de 2 carrés de la forme 4n+1) parmis tous les polygones ...(voir le chapitre sur : soit un polygone trouver le coté)
En résumé , il s'avère qu'une droite est de la forme 2n ou 2n+1 , un triangle est de la forme 3n/3, (3n+1)/3 ou (3n+2)/3 , un carré est de la forme 4n/4, (4n+1)/4,(4n+2)/4 ou (4n+3)/4 ...etc , la solution de ce problème est plus logique que mathèmatique
Décomposition d'un nombre triangulaire divisibilité par 2;
|
Soit le produit de deux nombres consécutifs x * (x+1) / 2 , un de ces deux nombres est divisible par 2 donc x = 2n ou x+1 = 2n , x = 2n-1
En clair , dans (x)(x+1) , x < x+1 , soit le nombre pair = x est le premier facteur et donc plus petit que x+1 impair , soit le nombre pair = x+1 est le deuxième facteur et donc le plus grand que x. Exemple x pair : 10*11/2 ,n=5, = 2(5)*[2(5)+1]/2 ; Exemple x+1 pair = 9*10/2 = [2(5)-1]*2(5)/2. |
Rappel N°1:
Un nombre triangulaire T(n) = n(n+1)/2 = la somme des nombres de 1 à n Exemple : T(7) = somme de 1 à 7 = 7*8/4 = 28 = 1+2+3+4+5+6+7 Rappel N°2: n Si vous n'êtes pas familier avec la notation de l'arithmétique modulaire cliquez sur ce lien pour un petit rappel
|
Décomposition d'un nombre triangulaire divisibilité par 2 * 3;
Soit le produit de deux nombres consécutifs x * (x+1) / 2 alors : x est divisible par 3 ou (x+1) est divisible par 3 ou aucun des deux !!! , si aucun des deux est divisible par 3 , (x-1) et (x+2) sont tout les deux divisible par 3 et un seul des deux est pair !!!
Résumons ce charabia dans un tableau:
|
|
|
||||
|
2n-2 |
2n - 1 |
2n |
2n |
2n+1 |
2n+2 |
|
2n - 2 = 6n' - 6 |
2n-1 = 6n'-3 |
2n = 6n' |
2n = 6n' |
2n+1 = 6n'+3 |
2n + 2 = 6n' + 6 |
|
=
n''=(n'-1) =>
|
=
|
=
|
=
|
=
|
=
n''=(n'+1) =>
|
|
si l'on applique (voir clef1 3ème paragraphe) : |
|||||
|
|
|
|
|
 |
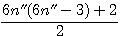 |
en cours de rédaction
|
Retour vers |
Page générale de tous les détails des équations |
Patrick Stoltz , La clef de Fermat : première publication du 5 mars 2015 / contact (ou coup de main) sur Twitter ou Email : pstoltz@shemath.com
rubrique petit théoréme 01/2016 et solutions 4n+1 04/2016
 , p premier
, p premier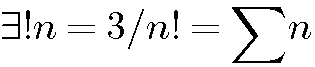
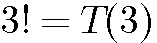
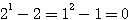
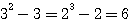
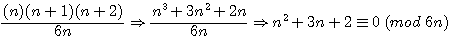
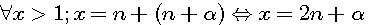
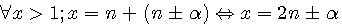
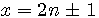
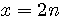
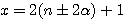
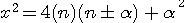
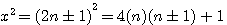
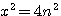
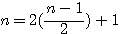 , par exemple 13 = 2(13-1/2)+1 => 13 = 2(6)+1 ; ceci étant toujours vrai pour un nombre pair : 14 = 2(14-1/2)+1 => 14 = 14-1 +1 = 14
, par exemple 13 = 2(13-1/2)+1 => 13 = 2(6)+1 ; ceci étant toujours vrai pour un nombre pair : 14 = 2(14-1/2)+1 => 14 = 14-1 +1 = 14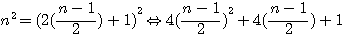
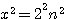
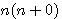 alors
alors 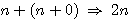
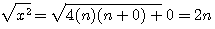
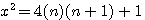 , c'est a dire quatre fois le produit d'un nombre
, c'est a dire quatre fois le produit d'un nombre 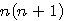 moins un.
moins un. 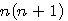 alors n+(n+1) = 2n +1 = x
alors n+(n+1) = 2n +1 = x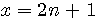
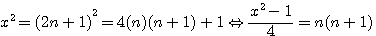
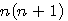 =>
=> 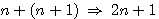 ;
;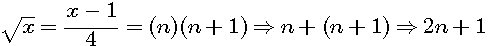
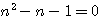
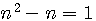
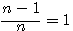
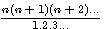 ,nous remplaçons n par 1 (n=1) alors :
,nous remplaçons n par 1 (n=1) alors :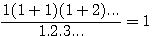
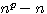 est divisible par p c'est à dire :
est divisible par p c'est à dire : 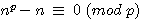
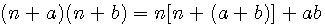
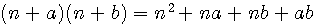
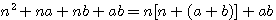
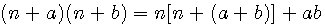
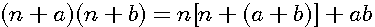
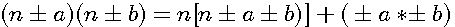
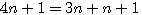
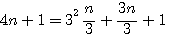
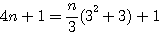
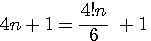
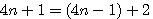
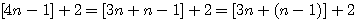
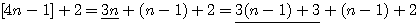
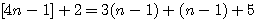
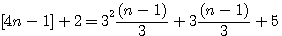
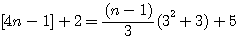
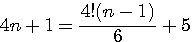
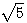 est une constante dans le nombre d'or et l'on observe que dans a²+b² premier a² ou b² l'un ou l'autre est divisible par 3,4 ou 5 ....
est une constante dans le nombre d'or et l'on observe que dans a²+b² premier a² ou b² l'un ou l'autre est divisible par 3,4 ou 5 .... 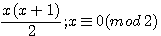
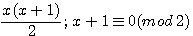
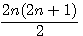
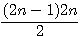
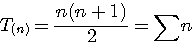
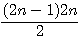
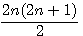
 0 (mod 3)
0 (mod 3)