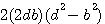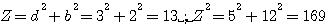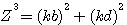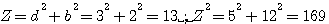|
page en cours de réalisation
Dans cette question Fermat ajoute une trés longue observation sur :
 I'hypoténuse de la forme 4n+1 est la somme de deux carrés; I'hypoténuse de la forme 4n+1 est la somme de deux carrés;
 Il évoque les nombres premiers; Il évoque les nombres premiers;
 Tous les exposants autre que 2. Tous les exposants autre que 2.
Livre III Question 4 : Trouver 3 nombres tels , que le carré de leur somme étant soustrait de chacun d'eux , les restes soient des carrés
En préambule à la question 22 , nous essayerons de mieux visualiser la méthode et la mise en équation des questions de Diophante:
Trouver 3 nombres tels , que le carré de leur somme étant soustrait de chacun d'eux , les restes soient des carrés
Solution . Soit N la somme des nombres que nous désignerons par 2n² , 5n² , 10n² , toutes les conditions du problème seront satisfaites si N=17N² , ou N=1/17
Diophante pose donc :
: 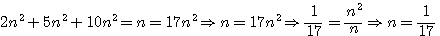
Le carré de leur somme : 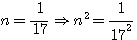
Remplaçons n² dans 2n² , 5n², 10 n² et additionons les :
|
1er nombre
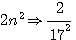
|
2ème nombre
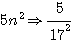
|
3éme nombre
|
La somme des 3 nombres
(= 1/17 = N la somme des nombres)
|
Le carré de leur somme
= 1/17² = N²
|
En posant n=17n2 Diophante obtient n = 17-1 , n² = 17-2 ... (il pose en fait 170n=17n2 )
Le carré de leur somme étant soustrait de chacun d'eux :
Livre III Question 22 : Trouver quatre nombres tels, que le carré de leur somme, augmenté ou dininué successivement de chacun d'eux, donne pour résultat un carré
Trouver quatre nombres tels, que le carré de leur somme, augmenté ou diminué successivement de chacun d'eux, donne pour résultat un carré.
Solution. Si on a un triangle rectangle dont l'hypothènuse soit a et les cotés b,c, puisque a²=b²+c² , a² +ou- 2bc sera un carré.
|
Il est difficile de comprendre , en parcourant l'arithmética, pourquoi Diophante écrit qu'une 'hypothénuse - 2n est un carré, tantôt d'hypothénuse (a+b)² - 4ab est un carré...Fermat réalisant même une "mise au carré" d'un nombre en lui ajoutant 2n+1...
Avant d'aborder la suite il faut tout d'abord comprendre pourquoi 2n-1 et non pas 2ab-b² , ce qui prouve bien que ce que nous avons démontré dans l'étude du livre 1 question 30 , si (a+b)²-(a-b)²=4ab alors il existe aussi une égalite (ab+1)² - (ab-1)² = 4ab, si ab = n alors (n²+1)²-(2n)²=(n-1)².
Emile Brassine écrit dans sa préface que la mise au carré d'un nombre est même une quasi obsession de Fermat.
Soit un triangle rectangle d'une hypothénuse c au carré c² ayant pour cotés x et y alors c²=a²+b² . Si l'on ajoute ou retranche 2ab alors nous obtenons:
 , c'est à dire un nouveau carré , c'est à dire un nouveau carré 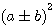
Prenons un exemple avec le triplet Pythagoricien de a=5 et b=12 une hypothénuse de 13² = a²+b².
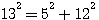 si nous lui ajoutons si nous lui ajoutons 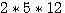 nous obtenons nous obtenons 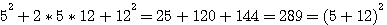
|
Pour résoudre notre problème, nous prendrons quatre triangles rectangles de même hypothénuse; cette hypothénuse multipliée par N représentera la somme des quatres nombres, qui seront les doubles produits des cotés de l'angle droit dans chaque triangle, multipliés par N², Or en décomposant de quatre manières 65 en deux carrés, on formera quatre triangles rectangles 65,39,52, ou 65,60,25 ou 65,63,16, ou 65,56,33.
Dans ce problème,Diophante , en décomposant 65 comme la somme de deux carrés trouve 4 possibilités pour une hypothénuse de 65.
|
65,39,52
Multiplication d'un triangle 3,4,5 par 13
|
65 = 13x5
|
39 = 13x3
|
52 = 13x4
|
|
65,60,25
Multiplication d'un triangle 13,12,5 par 5
|
65 = 5x13
|
60=5x12
|
25=5x5
|
|
65=8²+1²
Somme de deux carrés
|
65=8²+1²
|
63=8²-1²
|
16=2x8x1
|
|
65=7²+4²
Somme de deux autres carrés
|
65=7²+4²
|
33=7²-4²
|
56=2x7x4
|
Remarquez que 65 est la multiplication de 2 hypoténuse² : 13 (3²+2²=13) et 5 (2²+1²=5)
La somme des nombres sera 65.N, chaque nombre 2 x 39 x 52.N² , 2 x 60 x 25.N² , 2 x 63 x 16.N² , 2 x 56 x 33.N² , leur somme vaudra 12768.N² = 65N
(2 x 39 x 52.N²) + (2 x 60 x 25.N²) + (2 x 63 x 16.N²) + (2 x 56 x 33.N²) par factorisation = ( (2 x 39 x 52) + (2 x 60 x 25)+(2 x 63 x 16) + (2 x 56 x 33) )N² =12768.N² = 65N
|
,
N= 65/12768,
|
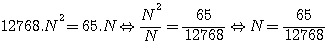 , en remplaçant n par sa valeur : , en remplaçant n par sa valeur : 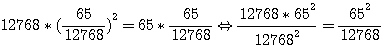
|
et les nombres cherchés seront des fractions dont les numérateurs égalent 17136600, 12 675000, 1565600 , 8517600. Le dénominateur commun 16 302 1824.
|
2x39x52x65²=17136600
|
2x60x25x65²=12675000
|
2x33x56x65²=15615600
|
2x63x16x65²=8517600
|
12768²=163021824
|
Emile Brassine ajoute le commentaire suivant:
Une formule générale qui donne une infinité de triangle, sans cesse employée par Diophante , est: 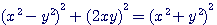 ; ;
Exemple , réalisons un triplet pithagoricien avec x=5 et y = 3 , nous obtenons bien (25-9)²+(2*5*3)²=(25+9)² => (16)²+(30)²=(34)² , mais x²+y² n'est pas une hypoténuse entière (5²+3² = 34 , 34 n'est pas une racine carré entière), entre autre parce que 30 (2*5*3) n'est pas un carré.
Afin de détailler cette observation de Emile Brassine, nous avons vu au préalable dans le livre 1 question 30 que: 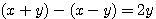 ; et que ; et que 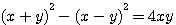
si n connait x,y on aura les éléments qui détermineront les cotés et l'hypothénuse; dans le problème actuel l'hypothénuse 65 est donnée et on la décompose en deux carrés de quatre manière, de telle sorte que 65 = x² + y², Par la suite de la détermination de x,y les cotés de l'angle droit sont connus.
65 Est la somme de 8² et 1² , et de 7² et 4² (49+16) , 65 est aussi égal au produit de 13 et 5 , c'est a dire (3²+2²) x (2²+1²) ; Ce qui m'a permis de produire le tableau ci dessus
|
OBS DE FERMAT. Un nombre premier qui surpasse de 1 tout multiple de 4 , est une seule fois l'hypothénuse d'un triangle rectangle (formé de cotés entiers),
Traduction : une hypoténuse de forme 4n+1 est qui est entière n'est qu'une seule fois l'hypoténuse entière d'un triangle rectangle.(Ce théorème est précisé sur la page Hypoténuse 4n+1 )
Exemple: soit le nombre premier 13 , est l'hypoténuse que d'un seul triangle rectangle de coté 12 et 5.
mais aussi 13 est aussi l'hypoténuse2 d'un triangle rectangle de coté 3 et 2 .(3²+2²=13)
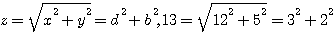
Comme le fait aussi Pierre de Fermat, je note par la suite, et pour une meilleure lecture et compréhension , les cotés de ce triangle "primaire" par les lettres d et b (au lieu de x' y') .
Je considère dans ce qui suit que d ou b  0 (mod 2) , pour éviter d'écrire 2d , b ou d , 2b 0 (mod 2) , pour éviter d'écrire 2d , b ou d , 2b
(Voir Hypoténuse 4n+1 )
|
|
Comme Pierre de Fermat , je désigne par la suite une hypoténuse par la lettre Z (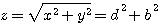 ): ):
et une hypoténuse carrée par z² : 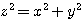
|
|
Seule possibilité
|
|
Z=13=3²+2² ,k=1
|
|
X=d²-b² = (d+b)(d-b)
X=3²-2²=5
|
Y=2db
Y=12
|
|
Z²=13²=5²+12²
|
|
|
son carré deux fois,
Première possibilité l'hypoténuse kz=k(d²+b²) : Le triangle rectangle de cotés kx et ky et 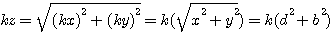
Exemple: kz=13x13=13²=169 , k=13 (pas d'autre possibilité puisque Z est premier !) , 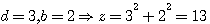 , donc un coté égal à 13x5 et l'autre coté 13x12 , donc un coté égal à 13x5 et l'autre coté 13x12
Dans l'exemple 134=(13(3²-2²))2+(13(2x3x2))2 = 65²+156²=169²
Deuxième possibilité l'hypoténuse z²=x²+y² : Par la formule
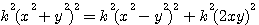 , k=1 alors , k=1 alors 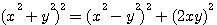
si 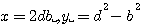 alors alors
les cotés de ce triangle rectangle sont 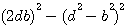 et et 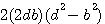
|
exemple : 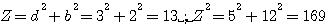
|
1ére possibilité (k=13)xZ
|
2éme possibilité (K=1)xZ²=1(x²+y²)
|
|
13x(3²+2²)=169
|
5²+12²=169
|
|
X=13(3²-2²)
13x5=65
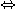
(13x3²)-(13x2²)
|
Y=13(2x3x2)
13x12=156
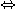
13(2x3x2)
|
(2bd)²-(d²-b²)²
12²-5²=119
|
2(2db)(d+b)(d-b)
2x12x5=120
|
|
X=65
|
Y=156
|
X=119
|
Y=120
|
Vérification : 1/ Z4 =134= 169²=65²+156² , 2/ Z4 =134=169²=119²+120²
|
|
son cube trois fois,
Première possibilité l'hypoténuse k²z=k²(d²+b²)
Dans cette premiére possibilité , si Z=d²+b² alors Z3 = k²z 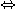 Z3=k²(d²+b²) Z3=k²(d²+b²) 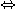 Z3=k²d²+k²b² Z3=k²d²+k²b²
Dans l'exemple ci-contre , Z=3²+2² (=13), 133 = 13²(3²+2²) qui fait , aprés développement , 133 = 13²3²+ 13²2²  133 = (13x3)²+(13x2)² 133 = (13x3)²+(13x2)²
Un cube , dont le coté est un nombre premier et est de type 4n+1  (4n+1)3 , est composé de 2 carrés kb et kd (4n+1)3 , est composé de 2 carrés kb et kd
Un nouveau triangle rectangle est ainsi composé de 2 nouveaux cotés (kb)²-(kd)² et 2(kb)(kd) .
Deuxième possibilité l'hypoténuse kz²=k(d²+b²)²
Troisième possibilité l'hypoténuse z²=x²+y² somme de deux carrés (sur l'exemple 46²+9²=133)
Z3 est la somme de 2 carrés dont j'ignore à ce jour comment Fermat le compose...
133 = 46² + 9² ... compose 2 nouveaux cotés 46²-9² et 2x46x9 ....
|
|
1ére : (k²=13²)xZ
|
2éme (K=13)xZ²
|
3éme Z3=x²+y²
|
|
13²x(3²+2²)=2197 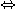
(13x3)²+(13x2)²=133 
39²+26²=133
|
13(12²+5²)=13x169
|
46²+9²=133
|
|
13²x5
39²-26²
|
13²x12
2x39x26
|
k(x²-y²)
13x119
|
k2xy
13x120
|
46²-9² |
2x46x9 |
| X=845 |
Y=2028 |
X=1547 |
X=1560 |
X=2035 |
Y=828 |
Pour 293 , je trouve 2 carrés qui le compose 145²+58²=293 ou 142²+65²=293
Le 1er cube est composé de (29x5)² et( 29x2)² , pour Z=(5²+2²)
|
|
sa quatrième puissance quatre fois, etc à l'infini.
|
|
|

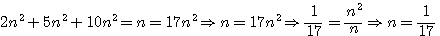
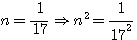
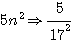
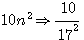
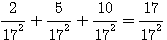
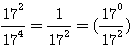
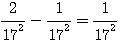 carré de
carré de 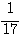
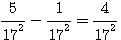 carré de
carré de 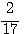
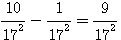 carré de
carré de 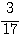
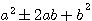 , c'est à dire un nouveau carré
, c'est à dire un nouveau carré 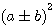
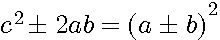
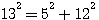 si nous lui ajoutons
si nous lui ajoutons 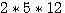 nous obtenons
nous obtenons 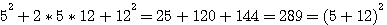
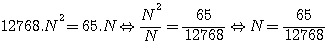 , en remplaçant n par sa valeur :
, en remplaçant n par sa valeur : 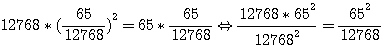
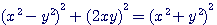 ;
;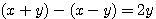 ; et que
; et que 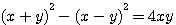
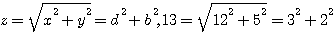
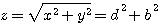 ):
): 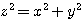
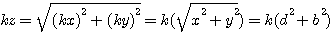
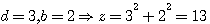 , donc un coté égal à 13x5 et l'autre coté 13x12
, donc un coté égal à 13x5 et l'autre coté 13x12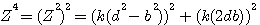
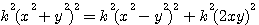 , k=1 alors
, k=1 alors 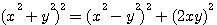
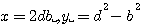 alors
alors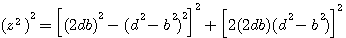
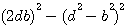 et
et