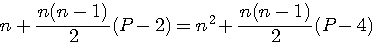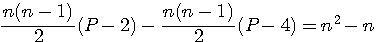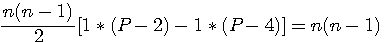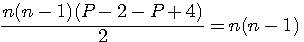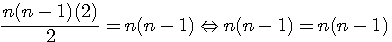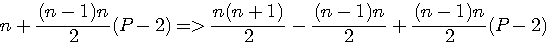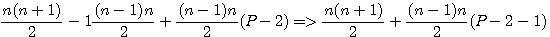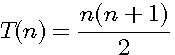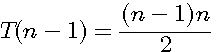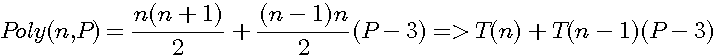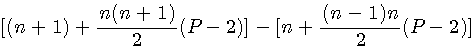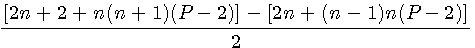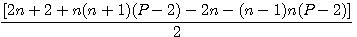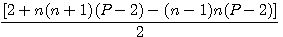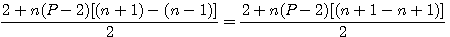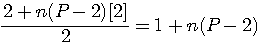Nombres Oblong |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
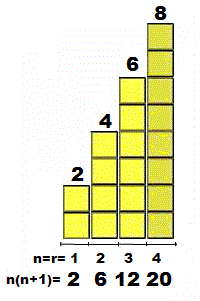
La suite des 4 premiers nombres pairs = 2+4+6+8 = 20
|
Un nombre Oblong est le produit de deux nombres entiers consécutifs s'exprime sous la forme n(n+1) = n²+n C'est la base de toute équation "Diophantesque" Ce nombre est égal à la somme des nombres pairs de 1 à n
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Nombres triangulaires = T |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
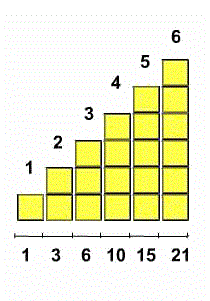
La suite des 6 premiers nombres entiers = 1+2+3+4+5+6 = 21 |
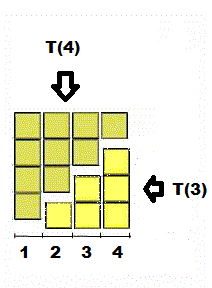
Un nombre triangulaire T(n) est le produit de deux nombres entiers consécutifs divisé par 2 Il s'exprime sous la forme T(n): Ce nombre T(n) est égal à la somme des nombres de 1 à n le n-ième nombre triangulaire est égal à la somme des n premiers entiers naturels non nuls exemple n=4 => T(4) = 1+2+3+4 = 10 est aussi égal à 4(4+1) / 2 = 20/2 = 10
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Nombres Triangulaires CARRE = TC(n) |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Un nombre triangulaire CARRE TC(n) est un nombre polygonal de base carré.TC(n) est la nième somme de nombres impairs Il s'exprime sous la forme TC(n): Exemple si r=n=4 : 2(1)-1 + 2(2)-1 + 2(3)-1 + 2(4)-1 = 4² => 1+3+5+7 = 4²
Observations
TC(3) = 3² = 9 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Rang = n ,le rang suivant = r+1Cette notion est trés subtile et merite un éclaircissement Si je prend par exemple 3² et que j'ajoute 2(3)-1 = 5 => 3² + 5 = 14 et non pas 16= 4² tout simplement parce que 2(r=3)-1 égale le "2n-1" du MEME rang Pour obtenir le carré n² suivant il faut ajouter 2(n+1)-1 . 3² + 2(4)-1 = 9 + 7 = 16 = 4²
Particulatité T(n) et TC(n)La somme d'un nombre triangulaire T(n) et de celui qui le suit T(n+1) est égal au triangulaire carré suivant TC(n+1) => T(n) + T(n+1) = TC(n+1) = (n+1)² |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
Démonstration:Développement
Regroupement
Division et identité remarquable
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
| La conjecture de Gaspard Bachet |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Les nombres Polygonaux
Les nombres polygonaux et Diophante
Tableau des nombres polygonaux
Cas particulier P=4 :
Les nombres polygonaux et Fermaten marge du théorème de Gaspard Bachet Pierre de Fermat propose une autre formule pour les nombres polygonaux : OBS de Fermat : Je rend cette proposition plus universelle. L'unité est le premier terme dans une progression quelconque de nombres polygonaux. Deux nombres consécutifs, augmentés du premier triangulaire , pris autant de fois qu'il y à d'angles dans le polygone moins quatre , font la seconde colonne ; Trois nombres consécutifs , augmentés du second triangulaire , pris autant de fois qu'il y a d'angle dans le polygone moins quatre , ferons la troisième colonne et ainsi de suite à l'infini Ce que Emile Brassine (1) traduit pas la formule : Equivalence des deux formules :Pour prouver que la formule originale de Diophante
Standardisation de la formule des nombres polygonaux
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Nombre polygonaux et relation de récurrenceNous remarquons que la formule: |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
RésuméLe polygonal(n+1) suivant de coté P égal ce polygonal (n) + n(P-2)+1 Fp(n+1,P)=Fp(n,P)+n(P-2)+1
Relation de récurrence: u(0)=1 ; u(n+1)=u(n)+n(P-2)+1
Particularité: Si P=3 =>u(n+1)=u(n)+(n+1) Exemple T(3) = 6 + (3+1) = 10 = T(4) Si P=4 =>u(n+1)=u(n)+(2n+1) TC(3) = 9 + (2*3+1) = 16 = TC(4) |
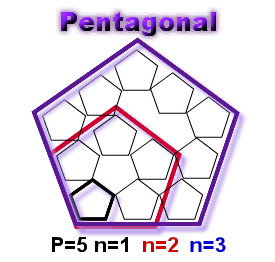
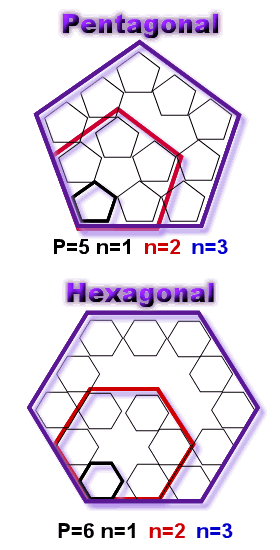
Sur le pentagonal ci contre le pentagonal n=3 est composé de 12 éléments . (que je figure par 12 petits pentagones) C'est à dire 1 élément = Fp(1,5) + 4 éléments =Fp(2,5) = 5 + 7 éléments = Fp(3,5) = 12 Ce qui serait intéressant se serait de savoir combien il faut que j'ajoute d'éléments pour obtenir le pentagonal suivant au lieu de calculer Fp(4,5)-Fp(3,5) Donc posons l'égalité:
Tout au même dénominateur
Suppression des parenthèses
+2n-2n s'annulent
Factorisation du deuxième et troisième terme par n(P-2)
dans (n+1-n+1) +n-n s'annulent
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Chapitre suivant les nombres poly-polygonaux 3D |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Un nombre poly-polygonal est un entier représentant non pas un polygone (plat) mais un parallélépipède (volume) divisé en un certain nombre. Par exemple 4x5x6 / 6 = 20 est une pyramide de base triangulaire formée de 20 pierres... |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
source:Oeuvres mathématiques et de l'arithmétique de diophante par E.Brassine (XIX éme siècle) aux éditions Jacques Gabay

Patrick Stoltz le 19/02/2009 – MAJ le 8/07/2010-13/01/2015 - 25/08/2019
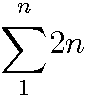
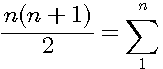

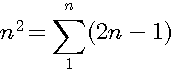
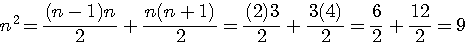
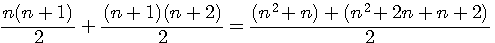
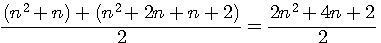
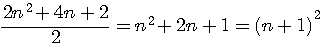

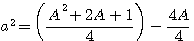 si K= (P-2) alors l'on obtient
si K= (P-2) alors l'on obtient 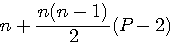
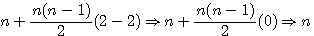
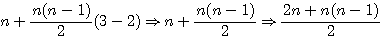
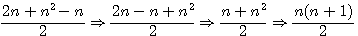
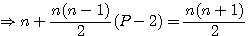
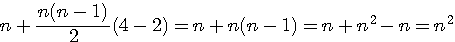 = TC(n)
= TC(n)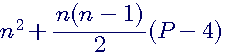
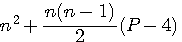 posons l'égalité .
posons l'égalité .