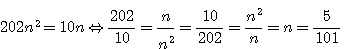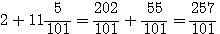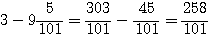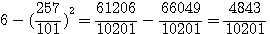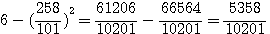|
|
 |
|||||||||
|
||||||||||
|
Livre V , Question 12 Diviser l'unité en deux parties telles que la somme de chaque partie et d'un nombre donné soit un carré.Solution. Soit le nombre donné 6 , chaque partie de l'unité plus 6 doit étre un carré ; la somme des deux carrés égale donc 13. Je désignerai par 2 +11N le coté du premier carré , et par 3-9N Le coté du second : la somme des carrés vaut 13 ou 202N² -10N+13=13;
d'où N=5/101 les cotés des carrés seront 257/101 , 258/101
, si de ces carrés nous otons 6, il restera pour les segments de l'unité 5358 / 10201 et 4843 / 10201
OBS DE FERMAT. Cette limitation est vraie et générale , puisqu'elle exclut tous les nombres inutiles ; il faut que le nombre donné ne soit pas impair et que le quotient de son double , augmenté d'une unité par le plus grand carré qui le mesure , ne puisse être divisé par aucun nombre premier égal à un multiple de 4 diminué de 1
|
||||||||||
|
d'aprés Fermat si x et y ne sont pas premier entre eux et qu'ils aient un facteur commun k, on aura 4n +1 = k²(x'² + y'²), par la suite (4n+1)/k² = x'² + y'² ; or le quotien du premier membre étant la somme de deux carrés , ne saurait être divisé par aucun nombre premier de la forme 4n-1, ce qui est encore un thèorème de Fermat.
Hypothénuse première:
Cette hypothénuse , composée de DEUX CARRES , (x et y) et si cette hypothénuse est un nombre premier alors ELLE N'EST PAS EGALE A K*Hypothénuse Exemple : Dans ce triangle rectangle K=13 :
|
||||||||||
|
|
||||||||||
|
sous rubriques de l'arithmética
|
||||||||||