Etude sur petit théorème de Fermat par la multiplication / division modulaire
| p | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27 | 28 | 29 | 30 | 31 | 32 | 33 | 34 | 35 | 36 | 37 |
| 0 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 | 1 |
| 21 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 2 |
| 22 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 | 4 |
| 23 | 1 | 0 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 | 8 |
| 24 | 2 | 0 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 | 16 |
| 25 | 4 | 0 | 5 | 2 | 10 | 8 | 6 | 4 | 2 | 0 | 15 | 14 | 13 | 12 | 11 | 10 | 9 | 8 | 7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | 32 | 32 | 32 | 32 | 32 |
| 26 | 1 | 0 | 1 | 4 | 9 | 4 | 12 | 8 | 4 | 0 | 13 | 10 | 7 | 4 | 1 | 20 | 18 | 16 | 14 | 12 | 10 | 8 | 6 | 4 | 2 | 0 | 31 | 30 | 29 | 28 | 27 |
| 27 | 2 | 0 | 2 | 8 | 7 | 8 | 11 | 2 | 8 | 0 | 9 | 2 | 14 | 8 | 2 | 18 | 13 | 8 | 3 | 24 | 20 | 16 | 12 | 8 | 4 | 0 | 29 | 26 | 23 | 20 | 17 |
| 28 | 0 | 4 | 6 | 3 | 4 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 4 | 14 | 3 | 16 | 6 | 22 | 13 | 4 | 24 | 16 | 8 | 0 | 25 | 18 | 11 | 4 | 34 | |
| 29 | 8 | 2 | 6 | 8 | 5 | 8 | 2 | 0 | 2 | 8 | 18 | 12 | 8 | 6 | 6 | 8 | 12 | 18 | 26 | 8 | 19 | 2 | 16 | 0 | 17 | 2 | 22 | 8 | 31 | ||
| 210 | 4 | 1 | 4 | 10 | 2 | 4 | 0 | 4 | 16 | 17 | 4 | 16 | 12 | 12 | 16 | 24 | 10 | 25 | 16 | 9 | 4 | 1 | 0 | 1 | 4 | 9 | 16 | 25 | |||
| 211 | 2 | 8 | 7 | 4 | 8 | 0 | 8 | 14 | 15 | 8 | 11 | 2 | 1 | 8 | 23 | 20 | 23 | 4 | 18 | 8 | 2 | 0 | 2 | 8 | 18 | 32 | 13 | ||||
| 212 | 4 | 1 | 8 | 1 | 0 | 16 | 10 | 11 | 16 | 1 | 4 | 2 | 16 | 21 | 14 | 19 | 8 | 7 | 16 | 4 | 0 | 4 | 16 | 1 | 28 | 26 | |||||
| 213 | 2 | 2 | 2 | 0 | 15 | 2 | 3 | 12 | 2 | 8 | 4 | 8 | 17 | 2 | 11 | 16 | 14 | 2 | 8 | 0 | 8 | 32 | 2 | 20 | 15 | ||||||
| 214 | 4 | 4 | 0 | 13 | 4 | 6 | 4 | 4 | 16 | 8 | 16 | 9 | 4 | 22 | 4 | 28 | 4 | 16 | 0 | 16 | 30 | 4 | 4 | 30 | |||||||
| 215 | 8 | 0 | 9 | 8 | 12 | 8 | 8 | 10 | 16 | 8 | 18 | 8 | 17 | 8 | 27 | 8 | 1 | 0 | 32 | 26 | 8 | 8 | 23 | ||||||||
| 216 | 0 | 1 | 16 | 5 | 16 | 16 | 20 | 9 | 16 | 11 | 16 | 7 | 16 | 25 | 16 | 2 | 0 | 31 | 18 | 16 | 16 | 9 | |||||||||
| 217 | 2 | 14 | 10 | 12 | 11 | 18 | 18 | 8 | 22 | 6 | 14 | 4 | 21 | 2 | 4 | 0 | 29 | 2 | 32 | 32 | 18 | ||||||||||
| 218 | 10 | 1 | 4 | 1 | 14 | 13 | 16 | 19 | 12 | 1 | 8 | 13 | 4 | 8 | 0 | 25 | 4 | 29 | 28 | 36 | |||||||||||
| 219 | 2 | 8 | 2 | 6 | 3 | 8 | 13 | 24 | 2 | 16 | 26 | 8 | 16 | 0 | 17 | 8 | 23 | 20 | 35 | ||||||||||||
| 220 | 16 | 4 | 12 | 6 | 16 | 1 | 22 | 4 | 4 | 23 | 16 | 1 | 0 | 1 | 16 | 11 | 4 | 33 | |||||||||||||
| 221 | 8 | 2 | 12 | 8 | 2 | 18 | 8 | 8 | 17 | 2 | 2 | 0 | 2 | 32 | 22 | 8 | 29 | ||||||||||||||
| 222 | 4 | 1 | 16 | 4 | 10 | 16 | 16 | 5 | 4 | 4 | 0 | 4 | 30 | 9 | 16 | 21 | |||||||||||||||
| 223 | 2 | 8 | 8 | 20 | 5 | 4 | 10 | 8 | 8 | 0 | 8 | 26 | 18 | 32 | 5 | ||||||||||||||||
| 224 | 16 | 16 | 14 | 10 | 8 | 20 | 16 | 16 | 0 | 16 | 18 | 1 | 28 | 10 | |||||||||||||||||
| 225 | 7 | 2 | 20 | 16 | 11 | 2 | 1 | 0 | 32 | 2 | 2 | 20 | 20 | ||||||||||||||||||
| 226 | 4 | 13 | 4 | 22 | 4 | 2 | 0 | 31 | 4 | 4 | 4 | 3 | |||||||||||||||||||
| 227 | 26 | 8 | 15 | 8 | 4 | 0 | 29 | 8 | 8 | 8 | 6 | ||||||||||||||||||||
| 228 | 16 | 1 | 16 | 8 | 0 | 25 | 16 | 16 | 16 | 12 | |||||||||||||||||||||
| 229 | 2 | 2 | 16 | 17 | 32 | 32 | 32 | 24 | |||||||||||||||||||||||
| 230 | 4 | 1 | 1 | 30 | 29 | 28 | 11 | ||||||||||||||||||||||||
| 231 | 2 | 2 | 26 | 23 | 20 | 22 | |||||||||||||||||||||||||
|
232 |
4 | 18 | 11 | 4 | 7 | ||||||||||||||||||||||||||
|
233 |
8 | 2 | 22 | 8 | 14 | ||||||||||||||||||||||||||
|
234 |
4 | 9 | 16 | 28 | |||||||||||||||||||||||||||
|
235 |
18 | 32 | 19 | ||||||||||||||||||||||||||||
|
236 |
28 |
1 |
Tableau des restes des puissances de 2
Résolution du petit théorème de fermat par la multiplication / division modulaire
La grande difficultée pour prouver et exploiter le petit théoréme de Fermat, pour la recherche des nombres premiers > 100 ,est que l'on dépasse vite la capacité des calculateurs courants.
A mon grand désarroi, j'avais conçu les divisions modulaires pensant qu'elle ne fonctionneraient que pour p premier , ce qui me permettrait de différencier les nombres premiers des non premiers dans le petit théorème de Fermat et sa réciproque sur les puissances de 2.
Je pouvait utiliser le même algorithme que ci-dessus , mais celà aurait crée autant d'itérations (boucle) que n...
Rappel conjecture : 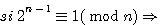 n est premier
n est premier
Les divisions modulaires fonctionnant pour tout p, il fallait trouver un autre moyen!!!
1/"Découpe" modulaire.

[Les inverses modulaires]
[Inv modulaire : Etude de fonctions]
[Div modulaire: Etudes des rationnels]
[Inv modulaire: Etudes des puissances]
[Div modulaire : PCDD-k-Bezoud]
[Div modulaire: Etude Nombres premiers]
Patrick Stoltz le 10/01/2011 – dépôt INPI en cours-
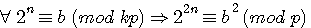
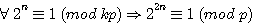
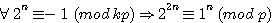
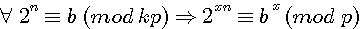

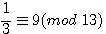 =>
=> 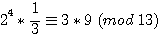 => 27
=> 27 

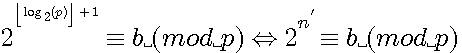
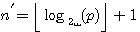
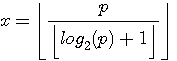
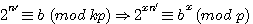
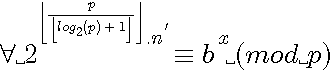
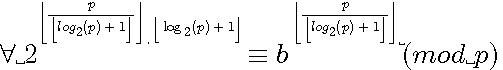
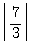 =2
=2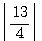 =3
=3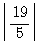 =3
=3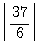 =6
=6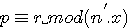
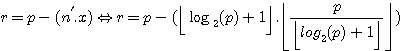
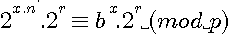
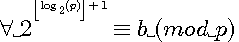
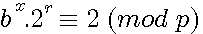 alors P est premier
alors P est premier