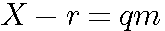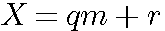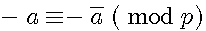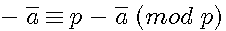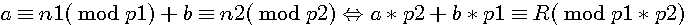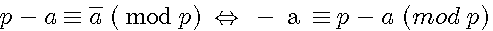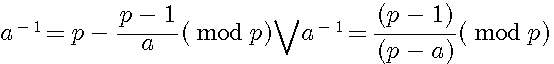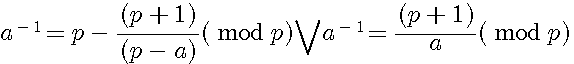Qu'est ce que de l'arithmétique modulaire ?

Définition mathématique:

L'arithmétique modulaire est une branche des mathématique utilisant un espace fini de nombres entiers.

Je resumerai cette définition comme étant l'étude du reste d'une division euclidienne dont cet espace serait limité par le diviseur.

Notation:

Soit une division euclidienne composée d'un Dividende divisé par le Diviseur , on obtient un quotient et éventuelement un reste.

En arithmétique modulaire on notera:

Et on dira :

Notez la différence , le Diviseur se situe à droite de l'expression ,après mod

L'on dit aussi Dividende appartient à la classe Reste modulo Diviseur

Division Euclidienne

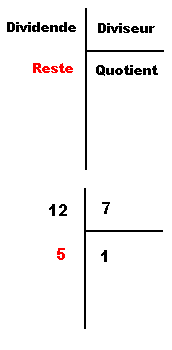
Exemple :

12 5 ( mod 7)

12 est congru 5 modulo 7

En arithmétique modulaire mod n'est pas une fonction (une fonction n'a qu'une image), mais limite le Dividende au Diviseur , reste étant le résultat de cette limite Diviseur.

Par exemple. Soit des minutes , elles sont limitées à 60mn dans une heures. Si je prends 90 mn alors nous écrivons : 90 30 (mod 60) qui veut dire  90 est congru à 30 (mod 60)

Ce que l'on peut représenter par: Si à partir de minuit , il s'ecoule 90 mn alors l'aiguille des minutes sera sur 30.

En résumé: Dividende  Reste (mod Diviseur) <=> modulo (Dividende/Diviseur) = Reste

A quoi ça sert ?

Nous utilisons tous les jours cette arithmétique pour compter les heures,minutes,secondes ,les angles...; Les ordinateurs utilisent aussi cette arithmétique puisque la capacité d'un processeur n'est pas infinie (exemple pour un ordinateur 64bits le nombre entier se limitera à +ou-2⁶³

Cette arithmétique est utilisée depuis la nuit des temps avec la division dite "Euclidienne"

C'est aussi la base du petit théoréme de Fermat sur les nombres premiers.

Important : On peut compter (modulo N) de 0 à N-1 , à N-1 on reprend à 0. Exemple si l'on compte les minutes, l'on compte de 0 à 59 minutes (et non pas de 0 à 60 minutes)

Où est le quotient ? Egalité arithmétique modulaire et Equation

Soit une division euclidienne représentée en arithmétique modulaire par Dividende  Reste (mod Diviseur) alors le Dividende - reste est divisible par quotient*diviseur

Exemple : soit 130 minutes , nous donne 130 10 (mod 60) = 130-10 0 (mod 60) qui veut dire 103mn-10mn est divisible par 2*(60mn = 1h)

Dans notre exemple : X-10mn = q*heures => X  10 (mod 60)

Dans la définition des anneaux modulaires , les couples de Dividende/Diviseurs donnant un reste 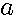sont appelés éléments de la classe 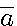, dans notre exemple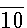

Arithmétique modulaire : Différences de notations et de logiques.

Division Euclidienne : Dividende/Diviseur => Quotient et Reste

Exemple: 90 minutes => 1 heure 30 minutes ; En arithmétique l'on calcule 90/60 ,1h est le quotient ,30 le reste des minutes.

L'opération division Euclidienne renvoie 2 nombres : Quotient et reste

L'on note que mathématiquement parlant , la division euclidienne n'est pas une fonction puisque renvoie 2 valeurs (images) et que par definition une fonction ne renvoie qu'une image.

Informatique (ou calculatrices): modulo(Dividende;Diviseur) => Reste

La fonction informatique modulo renvoie une seule valeur : le reste du couple (Dividende ; Diviseur) , pour connaître le quotient il faut utiliser une autre fonction : la partie entière d'une division : ENT(Dividende/diviseur)

L'on dit : le modulo (C.A.D le RESTE) de a et b = reste

Fonction modulo dans différents languages:

Opérations sur les nombres modulaires : Addition

Comme toute arithmétique, l'on peut ,sur les nombres modulaire, effectuer des opérations.

Exemple : Prenons un cercle en ° C.A.D mod 360°, ce qui est une bonne représentation de l'arithmétique modulaire et des nombres finis puisque nous ne nous préoccupons plus du nombre de cercles parcourus (quotient).

Programme PC

320°+90° = 410° divisé (*) par 360 ° il reste 50° (peu importe le nombre de cercles parcourus, ici 1 C.A.D 360°)

Donc 320°+90° 50° (mod 360°)

(*) La division étant une suite de soustractions , l'on aurait aussi faire 410°-360° = 50°

Dans l'exemple des angles , l'addition modulaire revient à ouvrir un l'angle ( Sens INVERSE des aiguilles d'une montre)

Exemples:

5+3 1 (mod 7) différent de 5+3=8 ...

6+3 2 (mod 7)

6+3=9 , 2 (mod 7)

7+2 0 (mod 9)

Exemple  : Avec des minutes: 110mn + 50 mn = 160mn , 160mn - 60mn = 100mn , 100mn - 60mn = 40mn

110mn + 50mn 40mn (mod 60mn)

Dans l'exemple des minutes , l'addition modulaire revient à avancer dans le temps ( Sens des aiguilles d'une montre)

Egalité de l'addition

Exemples

: 320°+90° 50° (mod 360°)

=

320°+90°= 1*360° + 50° =410°

 :110 + 50 40mn (mod 60mn)

=

110+50=2*60+40 = 160mn

Opérations sur les nombres modulaires : Multiplication

La multiplication s'éffectue aussi sans problème puisqu'une multiplication est une suite d'additions , par exemple : 2+2+2+2=4*2=8

Calculons 20 * 4 (mod 60) : 20*4 = 80 . 80 20 (mod 60). Donc 20 * 4 20 (mod 60)

Autres exemples : 4*90 0 (mod 360) , 5*3 1 (mod 7)

En multiplication modulaire l'on effectue l'opération et l'on débarrasse le résultat du multiple du modulo

Factorielle

n! 0 (mod n)

Exemple 5! = 1*2*3*4*5. Cette série est divisible forcement par 5 donc

5! 0 (mod 5)

Particularités

si a*b 0 (mod a )

alors a*b 0 (mod b)

3x4 0 (mod 3)

 => 3x4 0 (mod 4)

un rectangle a*b est divisible

par a ou b

Egalité de la multiplication

Exemples:

: 4*60 60 (mod 180)

=

1*180 + 60 = 240

 :5*3 1 (mod 7)

=

5*3=2*7+1= 15

Opérations sur les nombres modulaires : Soustraction

En théorie il suffirait de soustraire le nombre pour obtenir sa congruence.

Exemple 320-40 = 280 , nous écrivons , 320-40 280 (mod 360) , vérifions en ajoutant l'opposé du nombre -40 C.A.D + 40 :320-40(+40) 280(+40) (mod 360) <=> 320 320 (mod 360)

En clair : 320°-40° = 280° , 280°+40° = 320° ; Si je retire 40° à un angle, à ce resultat , si je rajoute 40° je doit retrouver le même angle.

Autre exemple : 5-3 2 (mod 7) <=> 5-3(+3) 2(+3) (mod 7) <=> 5 2 + 3  (mod 7) <=>5 5 (mod 7)  

En pratique ce n'est pas toujours vrai par exemple 9 -6  3 (mod 7) , si pour vérifier je rajoute 6 (de chaque coté de ) j'obtiens:

9  9 (mod 7) hors 9 2 (mod 7)...

En fait  9 -6  X (mod 7) est égal à :

[9  2 (mod 7)] - [6   6(mod 7)] =  2-6   -4 (mod 7)

C'est à dire une congruence négative...

Version "Classique" de la soustraction modulaire

Selon l'arithmétique modulaire, il faut ajouter de part et d'autre le nombre que l'on veut retrancher :

9-6(+6) n+(+6) (mod 7) => 2 n+6 (mod 7)

Quel est le nombre qui ajouté à 6 et divisé par 7 il reste 2 ?

qui s'ecrit : n+6 2 (mod 7) ?

si n  = 3 alors 2 (3+6) (mod 7) donc 9-6 3 (mod 7)

Principe des équations

si a-x=b alors

a-x(+x)=b(+x)

ce qui est équivalent à :

a-x=b <=> a=b+x

Exemple version "classique"

30-50 x (mod 60)

30  x +50 (mod 60)

Quel est le nombre qui ajouter à 50 30?

si x = 40 alors 40+50 30 (mod 60)

30-50 40 (mod 60)

Si à x heures 30mn je déduit 50mn alors il restera x-1 heures 40mn

Version logique : Résoudre une congruence négative si nécéssaire

Afin de rendre la soustraction modulaire beaucoup plus simple et logique: Si le resultat de la soustraction est négatif  il suffit de résoudre une congruence négative, par exemple : 30mn - 50mn = -20 mn  ? (mod 60)

( C'est à dire une autre soustraction modulaire : 0mn - 20 mn ? (mod 60)  )

Congruence négative = opposé modulaire

Cette particularité est utilisée tous les jours pour compter les minutes (sur une horloge)

Ainsi ne dit t'on pas il est 10h moins le quart ? les Anglais ne disent t'il pas it's quater to ten?

l'on écrirait donc : 60 - 15 n (mod 60) => 60 -15 45 (mod 60)

Bon évidement , il y à de fortes chances, si on vous demande l'heure et que vous répondiez il est 45 congru 60, l'on réagisse bizarrement...!!!

Si -a > p

Si par exemple je veux calculer - 130mm ( xheures - 130mn) alors je recule ma montre de 2 heures et il restera une certaine heure -10mn

2h - 130mn = minuit - 10

Pour calculer l'on effectue une division euclidienne 130 par 60 il reste 10 , si 130 est négatif , le reste est négatif

Exemple -[56 6 (mod 10)] = -56 -6 (mod 10)

Détails

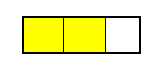
 20    20    20

(0) -20 40 (mod 60)

il faut 20 minutes pour aller à une heure pleine.

Sur cet exemple doit t'on considerer le temps en jaune (40 mn) ou en blanc (20 mn) ?

On peut dire il est 1h -20 (si l'on considère le blanc) ou 0 h 40 si l'on considère le jaune

Exemples

exemple : -160mn =

- [160mn 40mn (mod 60)]

= -160 -40mn (mod 60)

Autres exemples

-380° -20° (mod 360)

-56 -6 (mod 10)

-367 -7 (mod 60)

Si le négatif modulaire est > (mod p) alors , pour réaliser un modulo négatif, il faut au préalable calculer - son modulo positif

négatif modulaire dans sa classe (c'est à dire a<= p)

Etant donné que p 0 (mop p) => p-a 0 - a (mod p)

Exemples :

-380° -20° (mod 360°) puis

-380° 360°-20° (mod 360°)

-380° 340° (mod 360°)

-56 -6 (mod 10)

= -56 4 (mod 10)

-367 -7 (mod 60)

 -367 53 (mod 60)

Réaliser une soustraction modulaire

Pour réaliser une soustraction modulaire a-b r (mod p)

Réaliser la soustraction normalement => a-b r (mod p)

si r est négatif (c.a.d -r) alors convertir -r en +r en appliquant:

  -  a p - r (mod p)

Prenons l'exemple d'un cercle de 360° et réalisons 45°-180° :

45°-180°=-135° , -135° 225°(mod 360)

Exemples:

90mn - 10mn = 80mn

80 20 (mod 60)

45°-180° dans 1/4 cercle :

45°-180°=-135° 45° (mod 90)

Division modulaire

La division étant l'opération inverse d'une multiplication l'on écrit : si a*b  r (mod p) alors a r/b (mod p) =>  r/b a (mod p) ou b r/a (mod p) => r/a b (mod p)

Exemple : 21 = 7*3 1 (mod 10) donc nous pouvons écrire 1/7 3 (mod 10) ou 1/3 7 (mod 10)

Recherche "classique"

Soit ab     reste (mod p) représenté par la division modulaire Reste/b     a (mod p) nous connaissont Reste,b et p , nous recherchons a , ou vous l'avez bien compris maintenant,

Reste/a  b (mod p) nous connaissont Reste,a et p , nous recherchons b

Selon le principe de l'arithmétique modulaire, il faut multiplier de part et d'autre de le diviseur de Reste :

Soit r/a b (mod p), cherchons 5/3 b (mod 7) :

5/3(*3) b(*3) (mod 7) => 5 b*3 (mod 7) => 3b 5 (mod 7)

Quel est le nombre qui , multiplié par 3, est congru à 5 (mod 7) ?

vérification d'une division modulaire

ab Reste (mod Diviseur)

=

ab - Reste 0 (mod Diviseur)

Vérification de 5/3 4 (mod 7)

[5/3(*3)=5] [4(*3)=12] (mod 7)

<=> 5  12 (mod 7) =

12 5 (mod 7)

Résumé

r/a b (mod p) , multiplication par a:

r*a/a b*a (mod p) =

r ba mod (p) => ba  r mod (p)

on incremente b jusqu'à

ba - r  0 mod (p)

b = 4 car 4*3=12 , 12 5 (mod 7) donc 5/3  4 (mod 7) :

verifions par ab - reste  0 (mod p) => 3*4 - 5 0 (mod 7)

Programme (experimental) de calcul de division modulaire

Inverse modulaire 1/a b (mod p)   [ou  1/b a (mod p) ]

Soit une division modulaire reste/a b (mod p) étant égal à reste*1/a b (mod p), nous  cherchons en premier à multiplier reste par un inverse 1/a ce qui nous permettra d'utiliser 1 paramètre en moins :

reste/a b (mod p) nous oblige à utiliser reste , b et p pour rechercher a alors que (reste) * 1/a nous permet d'utiliser uniquement b et p pour rechercher a.

Pour réaliser ensuite une division modulaire reste*[1/a b (mod p)] x (mod p)

1/a b (mod p) <=> 1 ab (mod p) le dividende devient ab multiple de 2 nombres an dont le reste = 1 => ab 1 (mod p) . Et si ab 1 (mod p) = ab - 1 0 (mod p)

Cherchons 1/3  b (mod 10) => 3b 1 (mod 10) ,  3b-1 0 (mod 10) , b=7  => 21-1 0 (mod 10)

1/3 7 (mod 10) et aussi 1/7 3 (mod 10)

Egalité , définition de l'inverse modulaire

L'égalite d'un nombre modulaire étant :

Dividende - Reste  0 (mod Diviseur)

Dividende - Reste  = quotient*Diviseur

Nous pouvons définir un inverse modulaire par l'égalité suivante:

ab=Dividende , m = Diviseur , 1 = Reste

ab − 1 = qm  ( car p divise ab-1 )

Dans cette égalité a ou b et p sont connus , b ou a et q inconnus

Résumé :

Dividende = ab

Reste = 1

Quotient = q

Diviseur = mod=m

ab - 1 0 (mod p)

=

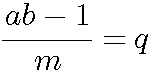
Si je reprends l'exemple 1/3 7 (mod 10) nous pouvons écrire :

3*7 - 1 = 2*10

En résumé :

Etude sur les inverses modulaires

remarque

Un inverse modulaire est aussi defini par l'égalité 1/a  = a/a² = a²/a³ .... modulo p )

Sens de comptage =  complément à deux

Différence entre valeur absolue et arithmétique modulaire:

En mathématique 40-50 = -10 l'oposé 50-40 = 10

En arithmétique modulaire, 40-50  50 (mod 60) ,l'opposé 50-40 10 (mod 60)

Dans cet exemple ,c'est le temps écoulé entre 0h 50mn et 1h 40 mn C.A.D 50 mn

(40-50) C.A.D -10  (mod 60)-10 (mod 60), si négatif 40-50  -10(+60) mod 60 =>ce qui est l'équivalent d'une retenue en soustraction.

L'arithmétique modulaire n'utilise que des nombres entiers naturels,(nombres uniquement positifs), ce qui implique de soustraire le plus grand - le plus petit et des retenues.

Si on lit :n 6 (mod 7)  n représente t'il -1 6 (mod 7) ou 6 6 (mod 7) , est ce -5 ou 2 2 (mod 7) ?

Nombres entiers relatifs

sens croissant -4,-3,-2,-1,0,1,2,3 ... sens décroissant 3,2,1,0,-1,-2,-3,-4

en modulo 7 sens croissant:

...,5,6,0,1,2,3,...

si les premiers chiffres représentent des nombres négatifs

-2,-1,0,1,2,3

en modulo 7 sens décroissant:

3,2,1,0,6,5,4 <=> -4,-5,-6,0,6,5,4

En résumé si l'on lit 5 l'on ne sait pas forcement si il représente 5 ou -2

La méthode juste est de considérer un nombre plus petit que la moitié du modulo comme un nombre négatif et plus grand que sa moitié comme un positif:

Complément à deux

2 est bien 2 (mod 7) plus petit que la moitié de 7.

5 est -2 , 5 plus grand que la moitié.

Tweet to @schemath