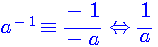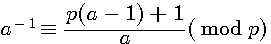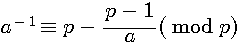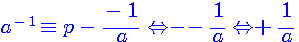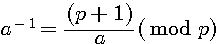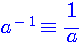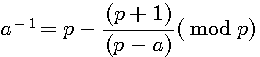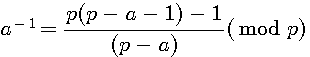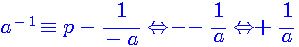|
|
 |
|
Préambule des inverses modulaires (mod N) - introduction des divisions dans les modulos de N |
|
|
Préambule , objectifs
Les nombres en l'arithmétique modulaire ne disposent que des opérations +,-,* pour des nombres entiers, la division n'étant définie comme impossible , ou éventuellement possible avec un modulo premier, les nombres modulaires ne disposants plus que de l'addition et la soustraction pour les réels.
Pour définir une division modulaire , nous cherchons en premier à multiplier un inverse ce qui nous permettra de chercher un paramètre au lieu de deux. Exemple a/b nous oblige à chercher a et b (mod p) alors que a * 1/b nous permet de chercher uniquement b (mod p)
Comme il n'est pas possible de diviser un nombre entier en arithmétique modulaire , il nous est donc impossible de manipuler des équations avec les congruences. Il nous importe donc de trouver une égalité avec un seul paramètre pour pouvoir manipuler les termes de cette équation avec les 4 opérateurs.
Voir toutes les explications détaillées au chapitre précédent.
Selon mes recherches sur le sujet, à l'heure actuelle, un inverse modulaire est défini par l'égalité suivante :
Sommaire et liens de l'étude détaillée:
Les Inverse modulaire et racine nièmes modulaires A quelle puissance faut t'il élever un nombre pourqu'il se termine par ce même nombre? ..... C.A.D 2n = ......2 , 3n = .....3 etc Les fonctions récurentes de type (p-1)
|
|
Resumé des fonctions |
|
|
J'ai défini au chapitre précédent 2 fonctions et leurs complèments que je nomerais les fonctions de type "p-1" et les fonctions de type "p+1". Ces 4 fonctions ont pour but de trouver un inverse modulaire entier < à P de type 1/a
Fonctions des "p - 1" et leurs équivalents en terme de congruence |
|
|
Comme p-1
|
ou
L'équivalent est:
|
Fonctions des "p + 1" |
|
|
L'équivalent est:
|
ou
L'équivalent est:
|
Nota 1: Selon la topologie des rectangles vu au chapitre précédent, ces équivalences justifieraient l'emploi de quatre fonctions pour définir le même inverse 1/a.
Nota 2: Il est possible , voir probable , qu'il existe d'autres fonctions pour définir un inverse négatif du type -1/a , exemple
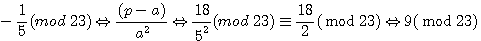
Matrices des a-1 (de p=7 à p=14) |
|
mod 7 |
mod 8 |
mod 9 |
mod 10 |
|||||||||||||
| 1/ |
type p-1 |
type p+1 |
type p-1 |
type p+1 |
type p-1 |
type p+1 |
type p-1 |
type p+1 |
||||||||
| 2 |
6 /5 |
4 |
4 |
27 /5 |
7 /6 |
9 /2 |
9 /2 |
39 /6 |
8 /7 |
5 |
5 |
53 /7 |
9 /8 |
11 /2 |
11 /2 |
69 /8 |
| 3 |
6 /4 |
5 |
8 /3 |
5 |
7 /5 |
17 /3 |
3 |
31 /5 |
8 /6 |
19 /3 |
10 /3 |
44 /6 |
9 /7 |
7 |
11 /3 |
59 /7 |
| 4 |
2 |
22 /4 |
2 |
13 /3 |
7 /4 |
25 /4 |
9 /4 |
23 /4 |
8 /5 |
7 |
10 /4 |
7 |
9 /6 |
31 /4 |
11 /4 |
49 /6 |
| 5 |
3 |
29 /5 |
8 /5 |
3 |
7 /3 |
33 /5 |
9 /5 |
5 |
2 |
37 /5 |
2 |
26 /4 |
9 /5 |
41 /5 |
11 /5 |
39 /5 |
| 6 |
6 |
6 |
8 /6 |
6 |
7 /2 |
41 /6 |
9 /6 |
7 /2 |
8 /3 |
46 /6 |
10 /6 |
17 /3 |
9 /4 |
51 /6 |
11 /6 |
29 /4 |
| 7 |
6 |
43 /7 |
8 /7 |
6 |
7 |
7 |
9 /7 |
7 |
4 |
55 /7 |
10 /7 |
4 |
3 |
61 /7 |
11 /7 |
19 /3 |
| 8 |
7 |
57 /8 |
9 /8 |
7 |
8 |
8 |
10 /8 |
8 |
9 /2 |
71 /8 |
11 /8 |
9 /2 |
||||
| 9 |
8 |
73 /9 |
10 /9 |
8 |
9 |
9 |
11 /9 |
9 |
||||||||
| 10 |
9 |
91 /10 |
11 /10 |
9 |
||||||||||||
|
mod 11 |
mod 12 |
mod 13 |
mod 14 |
|||||||||||||
|
type p-1 |
type p+1 |
type p-1 |
type p+1 |
type p-1 |
type p+1 |
type p-1 |
type p+1 |
|||||||||
| 2 |
10 /9 |
6 |
6 |
87 /9 |
11 /10 |
13 /2 |
13 /2 |
107 /10 |
12 /11 |
7 |
7 |
129 /11 |
13 /12 |
15 /2 |
15 /2 |
153 /12 |
| 3 |
10 /8 |
23 /3 |
4 |
76 /8 |
11 /9 |
25 /3 |
13 /3 |
95 /9 |
12 /10 |
9 |
14 /3 |
116 /10 |
13 /11 |
29 /3 |
5 |
139 /11 |
| 4 |
10 /7 |
34 /4 |
3 |
65 /7 |
11 /8 |
37 /4 |
13 /4 |
83 /8 |
12 /9 |
10 |
14 /4 |
103 /9 |
13 /10 |
43 /4 |
15 /4 |
125 /10 |
| 5 |
10 /6 |
9 |
12 /5 |
9 |
11 /7 |
49 /5 |
13 /5 |
71 /7 |
12 /8 |
53 /5 |
14 /5 |
90 /8 |
13 /9 |
57 /5 |
3 |
111 /9 |
| 6 |
2 |
56 /6 |
2 |
43 /5 |
11 /6 |
61 /6 |
13 /6 |
59 /6 |
12 /7 |
11 |
14 /6 |
11 |
13 /8 |
71 /6 |
15 /6 |
97 /8 |
| 7 |
10 /4 |
67 /7 |
12 /7 |
8 |
11 /5 |
73 /7 |
13 /7 |
47 /5 |
2 |
79 /7 |
2 |
64 /6 |
13 /7 |
85 /7 |
15 /7 |
83 /7 |
| 8 |
10 /3 |
78 /8 |
12 /8 |
7 |
11 /4 |
85 /8 |
13 /8 |
35 /4 |
12 /5 |
92 /8 |
14 /8 |
51 /5 |
13 /6 |
99 /8 |
15 /8 |
69 /6 |
| 9 |
5 |
89 /9 |
12 /9 |
5 |
11 /3 |
97 /9 |
13 /9 |
23 /3 |
3 |
105 /9 |
14 /9 |
38 /4 |
13 /5 |
113 /9 |
15 /9 |
11 |
| 10 |
10 |
10 |
12 /10 |
10 |
11 /2 |
109 /10 |
13 /10 |
11 /2 |
4 |
118 /10 |
14 /10 |
25 /3 |
13 /4 |
127 /10 |
15 /10 |
41 /4 |
| 11 |
10 |
111 /11 |
12 /11 |
10 |
11 |
11 |
13 /11 |
11 |
6 |
131 /11 |
14 /11 |
6 |
13 /3 |
141 /11 |
15 /11 |
9 |
| 12 |
11 |
133 /12 |
13 /12 |
11 |
12 |
12 |
14 /12 |
12 |
13 /2 |
155 /12 |
15 /12 |
13 /2 |
||||
| 13 |
12 |
157 /13 |
14 /13 |
12 |
13 |
13 |
15 /13 |
13 |
||||||||
| 14 |
13 |
183 /14 |
15 /14 |
13 |
||||||||||||
Pour visualiser jusqu'à 50 utilisez :  (schemath.com/calc_mod.html)
(schemath.com/calc_mod.html)
Patrick Stoltz le 27/12/2010 – dépôt INPI 390953 290710 du 23/08/2010 publié sur schemath 07/2010

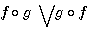
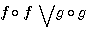
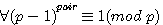 &
& 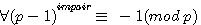
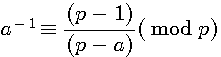
 -1 et p-a
-1 et p-a