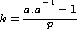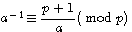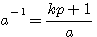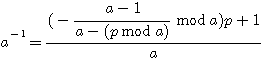
Recherche de k pour une image entière ou rationnelle d'un inverse modulaire
Préambule.Il faut noter que dans cette étude nous obtenons des inverses "primaire" , d'autres inverses (en modifiant k sont possibles). Exemple: 1/5 |
|
Formules générales de kSelon la définition des classes des nombre modulaires , nous savons que si a Mais aussi: Si a Exemple:a=26;p=7;r=5;k=3 => 7 = (26-5)/3 <=> 3 = (26-5)/7 C.A.D si 26
L'on note que si r < k ou p l'image de r ne change pas ( dans l'exemple 5 reste 5 et ne devient pas 2); Dans le cas d'inverses modulaires , le reste ne change jamais (toujours égal à 1) puisque toujours inférieur à p et k
|
(a-r)/p=k <=> (a-r)/k=p Exemple:a=26;p=7;r=5;k=3 7 = (26-5)/3 3 = (26-5)/7 |
Formules générales de k et inverses modulaires
|
|
|
Nous avons étudié K dans une forme a*a-1 Selon l'égalité a*a-1 = kp +1 en divisant par a l'on obtient .
Exemple: gimod(5,11) , image entière, Exemple: fimod(5,11) , image rationnelle
L'on note aussi que
ce qui implique que dans un système d'inverses modulaires : si kp+1 si a-1 est une image entière alors kp +1 est divisible par a
|
|
PGCD étendu et Coefficient de Bezoud |
|
|
Les coefficients de Bezoud representent le PGDC étendu d'un nombre sous la forme d'une équation ax + by = pgcd (a,b) voir détails sur PGCD étendus
Si a et b sont premiers entre eux alors ax + by =1. Si x est l'inverse modulaire de a modulo b alors
Ce qui confirme que:
|
1/Exemple avec des entiers , pgcd entre 33 et 50 (a=33 , p = 50) Avec la fontion 47 x 33 = 1551 Si l'on recherche k par la formule générale k=(1551-1)/50 ; k= 31 47x33 + (-50x31) = 1
|
L'indice (-kp) Pour qu'un inverse modulaire soit considéré comme indice k alors l'inverse modulaire doit etre Dans l'exemple ci dessus, si l'on recherche 1/50 mod 33 par les inverses modulaires, 50 étant congru à 17 modulo 33 => 1/17 -2
|
|
Raprochement des coefficients de bezoud et les inverses modulairesSi l'on assimile la formule de type "p+1",
|
|

Patrick Stoltz le 181/0/2009 – dépôt INPI en cours-
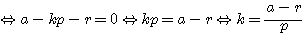
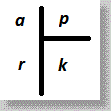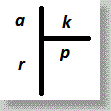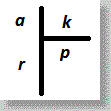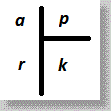
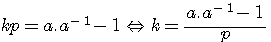
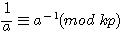 ?.
?.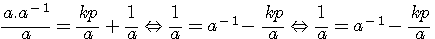
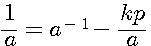
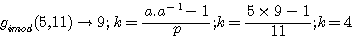
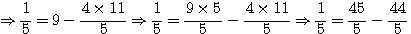
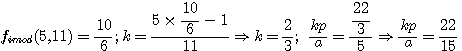
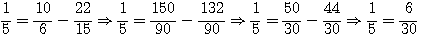
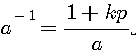
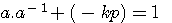 (a=a,a
(a=a,a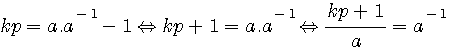
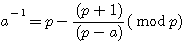 , l'on obtient 1/33
, l'on obtient 1/33