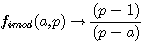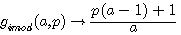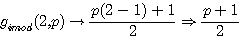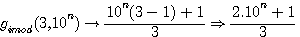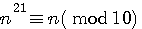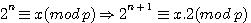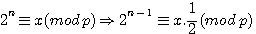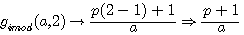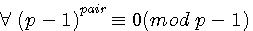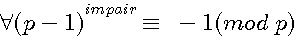Inv modulaire: Etudes des puissances

Puissances  modulo p et inverses modulaires

1/Egalité évidente

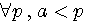
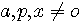      , pour tout p non divisible par a

si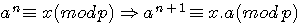

 

Exemple 23 1 (mod 7) , 24 1*2 (mod 7), 25 2*2 (mod 7)...

 

Voir tableau des modulos de puissances de 2 ci -dessous

 

2/Les inverses modulaires et les puissances:

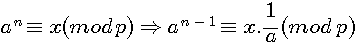
Rappel : a-1

1/2 modulo p , p impair (non divisible par 2)

Curiosité des cubes en base 10

La forme 2.....1 sera toujours divisible par 3 (c.q.f.d)

 

Exemple spectaculaire:

 

34 81 (mod 100) ,par gimod(3,100) => 1/3 67 (mod 100)

33 81*67 (mod 100) => 33 5427 (mod 100) => 542727 (mod 100)

32 27*67 (mod 100) => 33 1809 (mod 100) => 1809 9 (mod 100)

31 9*67 (mod 100) => 33 603 (mod 100) => 603 3 (mod 100)

30 3*67 (mod 100) => 30 201 (mod 100) => 201 1 (mod 100)

3-1 1*67 (mod 100) => 3-1 67 (mod 100)

L'on note que dans l'expression a b (mod k.p) pour ces puissances k=k*3

 

Exemple 1/2 (mod 7)

1/2 4 (mod 7)

25 4 (mod 7)

    

24 4*4 (mod 7)

24 16 (mod 7)

24 2 (mod 7)

23 2*4 (mod 7)

23 8 (mod 7)

23 1 (mod 7)

22 1*4 (mod 7)

22 1*4 (mod 7)

22 4 (mod 7)

21 4*4 (mod 7)

21 16 (mod 7)

21 2 (mod 7)

20 2*4 (mod 7)

20 8 (mod 7)

20 1 (mod 7)

2-1 1*4 (mod 7)

2-1 1*4 (mod 7)

2-1 4 (mod 7)

3/ inverses modulaires et fractions

En considérant l'égalité 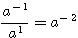l'on obtient une nouvelle vision des inverses modulaires

 

Exemple 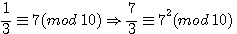. ou aussi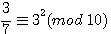

 

Le carré d'un nombre (7² dans l'exemple) peut être représenté par la fraction de ce nombre / inverse modulaire de ce nombre.

Inverse modulaire et racine nièmes modulaires

Grâce à la double vision d'un nombre (C.A.D une fraction et un nombre entier représenté par a-1) l'om peut extraire modulo n une racine

 

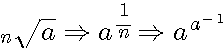
La racine niéme de a est égal à  a 1/n qui est égal à a puissance sa representation entiére d'un inverse modulaire

exemple :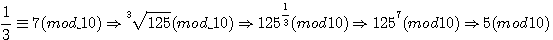

(125 7 = 476837158203125)

 

Petite enigme amusante:

A quel puissance faut t'il élever un nombre pourqu'il se termine par ce même nombre? ..... C.A.D 2n = ......2 , 3n = .....3 etc

 

La réponse est ............... 21

 

Explication:

 

n1/3 x n1/3 x n1/3 = n3/3 = n

En multipliant une racine cubique 3 fois l'on obtient le nombre de départ

 

Puique la représentation de 1/3 7 (mod 10) donc :

 

n7 x n7 x n7 = n (mod 10)

 

 
121 =1

221

=2097152

321

=10460353203

421

=4398046511104

521

=476837158203125

621

=21936950640377856

721

=558545864083284007

821

=9223372036854775808

921

=109418989131512359209

 

Lecture de la matrice des puissances de 2

p 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37
0 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1 1
21 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2 2
22 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4 4
23 1 0 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8 8
24 2 0 7 6 5 4 3 2 1 0 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16 16
25 4 0 5 2 10 8 6 4 2 0 15 14 13 12 11 10 9 8 7 6 5 4 3 2 1 0 32 32 32 32 32
26 1 0 1 4 9 4 12 8 4 0 13 10 7 4 1 20 18 16 14 12 10 8 6 4 2 0 31 30 29 28 27
27 2 0 2 8 7 8 11 2 8 0 9 2 14 8 2 18 13 8 3 24 20 16 12 8 4 0 29 26 23 20 17
28
0 4 6 3 4 9 4 1 0 1 4 9 16 4 14 3 16 6 22 13 4 24 16 8 0 25 18 11 4 34
29

8 2 6 8 5 8 2 0 2 8 18 12 8 6 6 8 12 18 26 8 19 2 16 0 17 2 22 8 31
210


4 1 4 10 2 4 0 4 16 17 4 16 12 12 16 24 10 25 16 9 4 1 0 1 4 9 16 25
211



2 8 7 4 8 0 8 14 15 8 11 2 1 8 23 20 23 4 18 8 2 0 2 8 18 32 13
212




4 1 8 1 0 16 10 11 16 1 4 2 16 21 14 19 8 7 16 4 0 4 16 1 28 26
213





2 2 2 0 15 2 3 12 2 8 4 8 17 2 11 16 14 2 8 0 8 32 2 20 15
214






4 4 0 13 4 6 4 4 16 8 16 9 4 22 4 28 4 16 0 16 30 4 4 30
215







8 0 9 8 12 8 8 10 16 8 18 8 17 8 27 8 1 0 32 26 8 8 23
216








0 1 16 5 16 16 20 9 16 11 16 7 16 25 16 2 0 31 18 16 16 9
217









2 14 10 12 11 18 18 8 22 6 14 4 21 2 4 0 29 2 32 32 18
218










10 1 4 1 14 13 16 19 12 1 8 13 4 8 0 25 4 29 28 36
219











2 8 2 6 3 8 13 24 2 16 26 8 16 0 17 8 23 20 35
220












16 4 12 6 16 1 22 4 4 23 16 1 0 1 16 11 4 33
221













8 2 12 8 2 18 8 8 17 2 2 0 2 32 22 8 29
222














4 1 16 4 10 16 16 5 4 4 0 4 30 9 16 21
223















2 8 8 20 5 4 10 8 8 0 8 26 18 32 5
224
















16 16 14 10 8 20 16 16 0 16 18 1 28 10
225

















7 2 20 16 11 2 1 0 32 2 2 20 20
226


















4 13 4 22 4 2 0 31 4 4 4 3
227



















26 8 15 8 4 0 29 8 8 8 6
228




















16 1 16 8 0 25 16 16 16 12
229





















2 2 16
17 32 32 32 24
230






















4 1
1 30 29 28 11
231























2
2 26 23 20 22

232

























4 18 11 4 7

233

























8 2 22 8 14

234


























4 9 16 28

235



























18 32 19

236




























28

1

Tableau des restes des puissances de 2 (mod p) par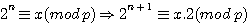

pour open office =MOD(cellule_du_dessus*2;p)

L'on observe:

Pour les nombres impairs:

Soit une série répétitive , Soit des séries répétitive ou unique (et de ce fait les modulos contiennent tout n)

Pour les nombres pairs:

Si divisible par 4 les modulos "tombent" à 0

Lecture de cette matrice - déplacement (vertical) 2n+1 2n-1

 

Déplacement "positif" dans la matrice 2n

 

si

et ceux pour tout P

Exemples:

27 2 (mod 21) => 28 4 (mod 21)

L'on note que pour cet exemple p n'est pas premier

 

Ce principe s'applique aussi si la congruence est > p

25 11 (mod 21) => 26 11*2 (mod 21) => 26 22 (mod 21)

22 1 (mod 21) => 26 1 (mod 21)

 

Déplacement "négatif" dans la matrice 2n

 

Si l'on applique 1/2 sur gimod(a,2)

L'on obtient un nombre entier si P est impair

 

par gimod(11,2) 1/2 11 (mod 21)

 

Exemples:

26 1 (mod 211) => 26-1 1*11 (mod 21) => 25 11 (mod 21)

L'on note que pour cet exemple p n'est pas premier

 

Ce principe s'applique aussi si la congruence est > p

27 2 (mod 21) => 27-1 2*11 (mod 21) => 26 1 (mod 21)

 

Les Fonctions récurrentes sur fimod(a,p) et les puissances

 

 

p  (p-1)2 (mod p) k (p-1)4 (mod p)

k

 (p-1)6 (mod p) k
2 1 1
1 1
1 1
3 4 1 1 16 1 5 64 1 21
4 9 1 2 81 1 20 729 1 182
5 16 1 3 256 1 51 4096 1 819
6 25 1 4 625 1 104 15625 1 2604
7 36 1 5 1296 1 185 46656 1 6665
8 49 1 6 2401 1 300 117649 1 14706
9 64 1 7 4096 1 455 262144 1 29127
10 81 1 8 6561 1 656 531441 1 53144
11 100 1 9 10000 1 909 1000000 1 90909
12 121 1 10 14641 1 1220 1771561 1 147630
13 144 1 11 20736 1 1595 2985984 1 229691
14 169 1 12 28561 1 2040 4826809 1 344772
15 196 1 13 38416 1 2561 7529536 1 501969
16 225 1 14 50625 1 3164 11390625 1 711914
17 256 1 15 65536 1 3855 16777216 1 986895
18 289 1 16 83521 1 4640 24137569 1 1340976
19 324 1 17 104976 1 5525 34012224 1 1790117
20 361 1 18 130321 1 6516 47045881 1 2352294
21 400 1 19 160000 1 7619 64000000 1 3047619
22 441 1 20 194481 1 8840 85766121 1 3898460
23 484 1 21 234256 1 10185 113379904 1 4929561
24 529 1 22 279841 1 11660 148035889 1 6168162
25 576 1 23 331776 1 13271 191102976 1 7644119
26 625 1 24 390625 1 15024 244140625 1 9390024

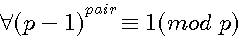
Ce théorème peut aussi logiquement et simplement s'expliquer dans le développement du polynôme 

(p-1)n pair

 

(p-1)2 = (p² -2p +1)

(p-1)4 = (p4-4p3+6p2-4p+1)

(p-1)6 = (p6-6p5+15p4-20p3+15p2-6p+1)

...

Tous les coefficients (table de Pascal) sont des multiples de p donc congrus p sauf le dernier qui est toujours égal à +1

 

 

Je note :

 

 

 

K= ((p-1)n pair -1)/P

 

p  (p-1)3

(mod p)

 k

(p-1)5

(mod p)

k

(p-1)7

(mod p)

 k
2 1 1
1 1
1 1
3 8 2 2 32 2 10 128 2 42
4 27 3 6 243 3 60 2187 3 546
5 64 4 12 1024 4 204 16384 4 3276
6 125 5 20 3125 5 520 78125 5 13020
7 216 6 30 7776 6 1110 279936 6 39990
8 343 7 42 16807 7 2100 823543 7 102942
9 512 8 56 32768 8 3640 2097152 8 233016
10 729 9 72 59049 9 5904 4782969 9 478296
11 1000 10 90 100000 10 9090 10000000 10 909090
12 1331 11 110 161051 11 13420 19487171 11 1623930
13 1728 12 132 248832 12 19140 35831808 12 2756292
14 2197 13 156 371293 13 26520 62748517 13 4482036
15 2744 14 182 537824 14 35854 105413504 14 7027566
16 3375 15 210 759375 15 47460 170859375 15 10678710
17 4096 16 240 1048576 16 61680 268435456 16 15790320
18 4913 17 272 1419857 17 78880 410338673 17 22796592
19 5832 18 306 1889568 18 99450 612220032 18 32222106
20 6859 19 342 2476099 19 123804 893871739 19 44693586
21 8000 20 380 3200000 20 152380 1280000000 20 60952380
22 9261 21 420 4084101 21 185640 1801088541 21 81867660
23 10648 22 462 5153632 22 224070 2494357888 22 108450342
24 12167 23 506 6436343 23 268180 3404825447 23 141867726
25 13824 24 552 7962624 24 318504 4586471424 24 183458856
26 15625 25 600 9765625 25 375600 6103515625 25 234750600

 

développement du polynôme (p-1)n impair

 

(p-1)3 = (p3-3p2+3p-1)

(p-1)5 = (p5-5p4+10p3-10p2+5p-1)

(p-1)7 = (p7-7p6+21p5-35p4+35p3-21p2+7p-1)

 

Tous les coefficients (table de Pascal) sont des multiples de p donc congrus p sauf le dernier qui est toujours égal à -1 <=> (p-1)

 

K= ((p-1)n impair - (p-1))/P

 

 
[Précédente][Index Arithmética][Suivante]

 

 

Patrick Stoltz le 10/01/2011 – dépôt INPI en cours-

pstoltz@shemath.com