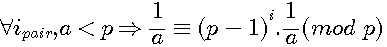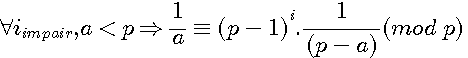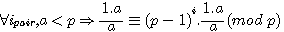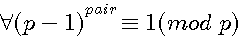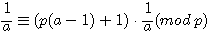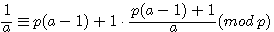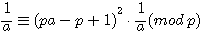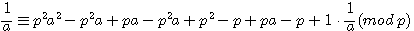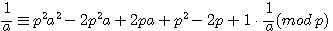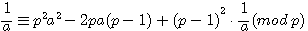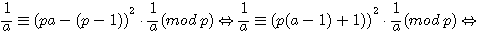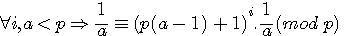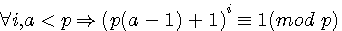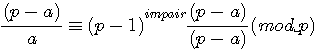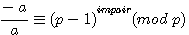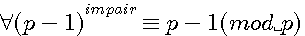Soit a , x,b,c < p ![]() pour tout p ,
pour tout p ,
Nous utiliserons pour cette etude la multiplication et addition , car nous n'avons pas encore défini a,x € Q
Matrices des a-1 (de p=5 à p=15) |
|
|
|
|
|
|
|
1/a |
mod 5 |
mod 6 |
mod 7 |
mod 8 |
mod 9 |
mod 10 |
mod 11 |
mod 12 |
mod 13 |
mod 14 |
mod 15 |
|||||||||||
1/2 |
4 /3 |
3 |
5 /4 |
7 /2 |
6 /5 |
4 |
7 /6 |
9 /2 |
8 /7 |
5 |
9 /8 |
11 /2 |
10 /9 |
6 |
11 /10 |
13 /2 |
12 /11 |
7 |
13 /12 |
15 /2 |
14 /13 |
8 |
1/3 |
2 |
11 /3 |
5 /3 |
13 /3 |
6 /4 |
5 |
7 /5 |
17 /3 |
8 /6 |
19 /3 |
9 /7 |
7 |
10 /8 |
23 /3 |
11 /9 |
25 /3 |
12 /10 |
9 |
13 /11 |
29 /3 |
14 /12 |
31 /3 |
1/4 |
4 |
4 |
5 /2 |
19 /4 |
2 |
22 /4 |
7 /4 |
25 /4 |
8 /5 |
7 |
9 /6 |
31 /4 |
10 /7 |
34 /4 |
11 /8 |
37 /4 |
12 /9 |
10 |
13 /10 |
43 /4 |
14 /11 |
46 /4 |
1/5 |
4 |
21 /5 |
5 |
5 |
3 |
29 /5 |
7 /3 |
33 /5 |
2 |
37 /5 |
9 /5 |
41 /5 |
10 /6 |
9 |
11 /7 |
49 /5 |
12 /8 |
53 /5 |
13 /9 |
57 /5 |
14 /10 |
61 /5 |
1/6 |
|
|
5 |
31 /6 |
6 |
6 |
7 /2 |
41 /6 |
8 /3 |
46 /6 |
9 /4 |
51 /6 |
2 |
56 /6 |
11 /6 |
61 /6 |
12 /7 |
11 |
13 /8 |
71 /6 |
14 /9 |
76 /6 |
1/7 |
|
|
|
|
6 |
43 /7 |
7 |
7 |
4 |
55 /7 |
3 |
61 /7 |
10 /4 |
67 /7 |
11 /5 |
73 /7 |
2 |
79 /7 |
13 /7 |
85 /7 |
14 /8 |
13 |
1/8 |
|
|
|
|
|
|
7 |
57 /8 |
8 |
8 |
9 /2 |
71 /8 |
10 /3 |
78 /8 |
11 /4 |
85 /8 |
12 /5 |
92 /8 |
13 /6 |
99 /8 |
2 |
106 /8 |
1/9 |
|
|
|
|
|
|
|
|
8 |
73 /9 |
9 |
9 |
5 |
89 /9 |
11 /3 |
97 /9 |
3 |
105 /9 |
13 /5 |
113 /9 |
14 /6 |
121 /9 |
1/10 |
|
|
|
|
|
|
|
|
|
|
9 |
91 /10 |
10 |
10 |
11 /2 |
109 /10 |
4 |
118 /10 |
13 /4 |
127 /10 |
14 /5 |
136 /10 |
1/11 |
|
|
|
|
|
|
a-1 |
a-1
|
|
|
|
|
10 |
111 /11 |
11 |
11 |
6 |
131 /11 |
13 /3 |
141 /11 |
14 /4 |
151 /11 |
1/12 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
11 |
133 /12 |
12 |
12 |
13 /2 |
155 /12 |
14 /3 |
166 /12 |
1/13 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
12 |
157 /13 |
13 |
13 |
7 |
181 /13 |
1/14 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
13 |
183 /14 |
14 |
14 |
1/15 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
14 |
211 /15 |
L'on constate
1/la réciprocité des deux fonctions (pour p premier ou non) pour leurs valeurs entières. Exemple 1/7 3 (mod 10) <=> 1/3
7 (mod 10)
2/ pour (p-1) les deux fonctions ont la même image (prouvé au chapitre précédent)
Trouver des valeurs entières pour a-1
fimod((p+1)/2) = 2(réciproque de la fonction ci contre)
|
gimod(2)=(p+1)/2
Si P est impair alors gimod(2,p)
|
gimod((p-2)=(p-1)/2(réciproque de la fonction ci contre)
Si P est impair alors fimod(p-2,p)
|
gimod((p-1)/2)=(p-2)
Si P est impair alors gimod((p-1)/2,p) |
Généralisation de a-1
f(a,p) et g(a,p) ont pour images deux solutions rationnelles vérifiant la congruence de l'inverse d'un nombre.
(Un inverse modulaire entier n'étant qu'un rationnel divisé par 1)
1/ Rappel a.a-1 congru 1
Dans la démonstration des inverses modulaires nous avions ax 1 (mod p) , x = a-1auquel nous ajoutions (p-1) pour obtenir une égalité.
donc 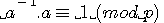
Si l'image de fimod(a,p) et gimod(a,p) n'est pas un entier alors un inverse modulaire à pour image une nouvelle division modulaire
|
|
|
Si une image d'une fonction est un rationnel alors , selon la réciprocité d'un inverse, il devient une multiplication d'un inverse
1/Congruence sur c
si 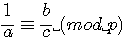 , par multiplication par a de part et d'autre de cette congruence (donc a/a
, par multiplication par a de part et d'autre de cette congruence (donc a/a 1 (mod p)
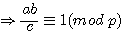
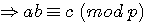
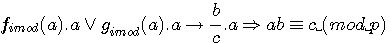
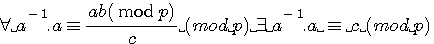
Si l'on multiplie de part et d'autre de la congruence par a alors les dividendes images de fimod(a) ou gimod(a) sont congrus au diviseur
Attention : ab est modulo P et non pas modulo c (dans le cas ou c=(p_a)
Exemple:
|
(3.11+7=40) |
|
de plus l'on note l'image particulière de gimod(a) ou b est directement congru à 1
si 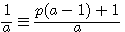 , l'expression p(x)+1 est toujours congrue à 1 , et c = a
, l'expression p(x)+1 est toujours congrue à 1 , et c = a
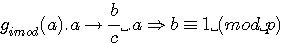
2/Congruence sur b
par multiplication par c :
si 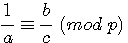 , par multiplication par c de part et d'autre de cette congruence :
, par multiplication par c de part et d'autre de cette congruence : 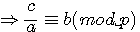
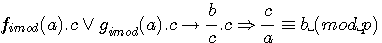
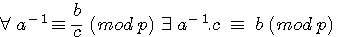
exemple:
|
ce qui par multiplication par a (4x7 congru 10) L'on note que comme 1/4 7/4 est bien congru a 10 par la multiplication des inverses |
|
Relation de récurrence sur les divisions modulaires
si l'imagefimod(a,p) et gimod(a,p) n'est pas entière alors un inverse modulaire à pour image une nouvelle division modulaire de la forme
Recurrence pour fimod(a,p) |
Recurrence pour gimod(a,p) |
|
Récurrence 0:
Récurrence 1:
(p-(p-a)) = a Récurrence 2:
Récurrence 3:
L'on peut donc généraliser cette récurrence par:
ce qui produit le théorème suivant: par multiplication par a
par la division modulaire et un exposant pair:
|
Récurrence 0:
Récurrence 1:
L'on peut donc généraliser cette récurrence par:
ce qui produit la conjecture suivante: par la division modulaire:
|
|
par la division modulaire et un exposant impair: multiplication par (p-a)
(p-a) = -a
par la division modulaire et un exposant impair:
|
|

Patrick Stoltz le 29/12/2010 – dépôt INPI 404167 040111
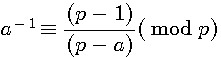
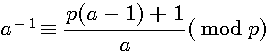
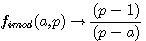
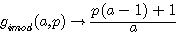

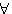 P impair
P impair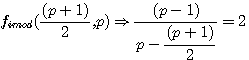
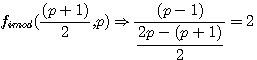
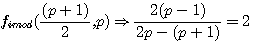
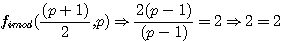
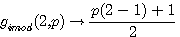
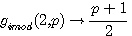
 P impair
P impair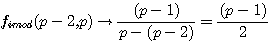
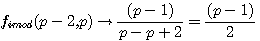
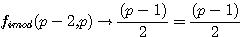
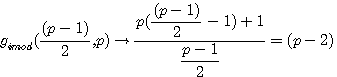
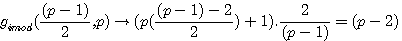
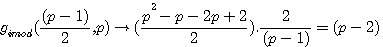
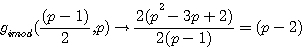
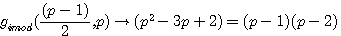
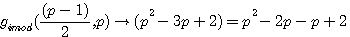
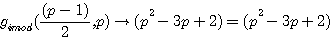
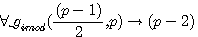


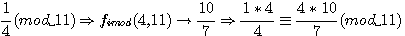
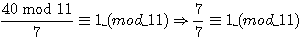
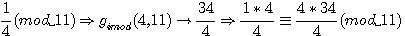
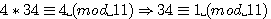
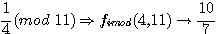
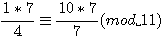
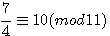
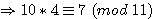
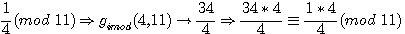
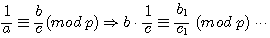
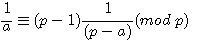

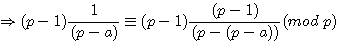
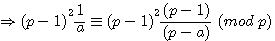
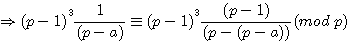 ...
...