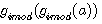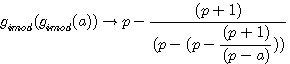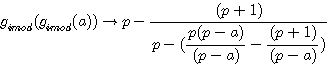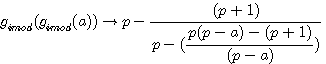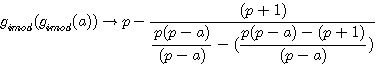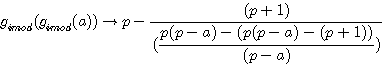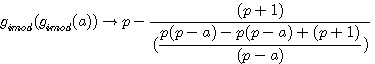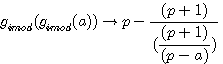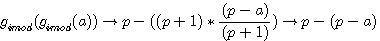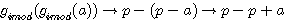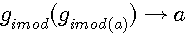Nous avons défini précédement que les inverses modulaires étaient définis par deux groupes de fonctions de type p-1 et p+1; Chaque groupe contenant deux fonctions.
Ce chapitre décrit les études de ces fonctions.(liens sur la page inverses modulaires :)
Sur la page ci dessous vous trouverez:
![]() Les recherches d'égalités entre les fonctions p-1
Les recherches d'égalités entre les fonctions p-1
![]() La réciprocité des fonctions de type p-1 ,
La réciprocité des fonctions de type p-1 , 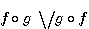
![]() La symétrie des fonctions de type p+1
La symétrie des fonctions de type p+1 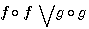
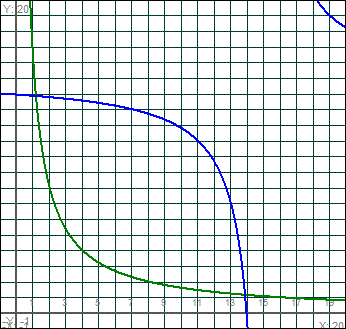
Graph des fonctions de type p-1 |
||||||||||||
|
||||||||||||
Égalité des deux fonctions fimod (a,p)= gimod (a,p) |
||||||||||||
Egalité entre les deux fonctions de type p-1 ?
suppression de -a , pa(a-1) , passage de -pa(a-1) à gauche de l'égalité
factorisation par pa à gauche de l'égalité
division par p de tous les termes
division par (a-1) les deux fonctions sont égales si et seulement si a = p-1
Une égalité simple entre les fonctions de type P+1 semble être moins simple p(p+1)=p²a-pa² Egalite entre fimod de type p-1 et de type p+1
|
||||||||||||
Etude d'égalités sur a-1 type p-1 |
||||||||||||
|
||||||||||||
Réciprocité des deux fonctions de type p-1 par
|
||||||||||||
|
||||||||||||
|
|
||||||||||||
|
Ces deux fonctions sont réciproques pour une valeur entière de a
L'on note que ce sont les deux fonctions qui sont réciproque l'une par rapport à l'autre ; C.A.D que l'on retrouve l'antécedent de l'une avec l'autre avec une valeur entiére. Nous verrons que cela est différent dans l'introduction des rationnels dans les nombres modulaire (image rationnelle de ces deux fonctions)
|
||||||||||||
Symétrie des fonctions de type p+1 par
|
||||||||||||
|
Ces deux fonctions sont symétrique et involutives pour une valeur entière de a
Dans ce type de fonction a à pour image le même nombre . Exemple pour p = 15 , f(4) à pour image 4 C.A.D (15+1)/4=4
|
P mis au même dénominateur (p-a)
P mis au même dénominateur (p-a)
Attention : signe - devant le groupe (p(p-a)-(p+1) = changement de signe
+p(p-a) et - p(p-a) s'annulent
Multiplication par l'inverse de (p+1)/(p-a)
Signe - devant (p-a)
|

Patrick Stoltz le 28/12/2010 – dépôt INPI 404167-040111
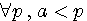
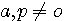
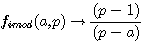
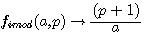
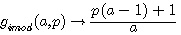
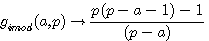





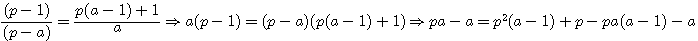
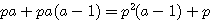
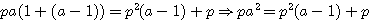
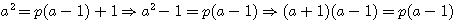
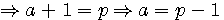
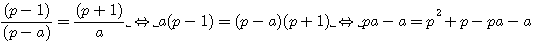
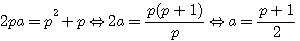
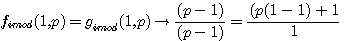
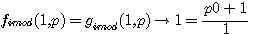
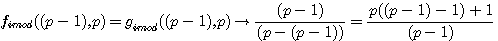
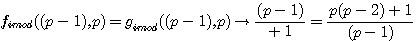
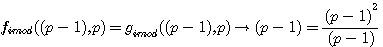
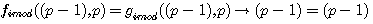
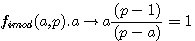
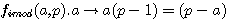
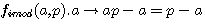
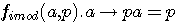
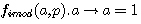
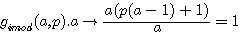
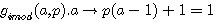
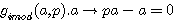
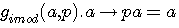
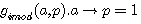
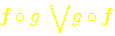
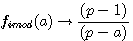 réalisons:
réalisons: 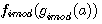
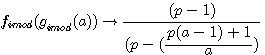
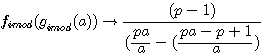
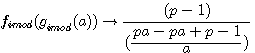
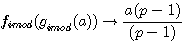
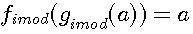
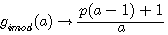 réalisons
réalisons 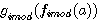
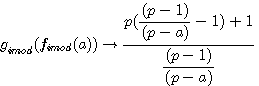
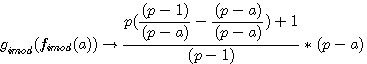
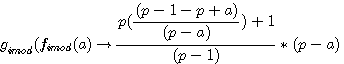
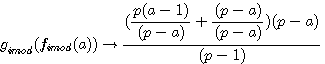
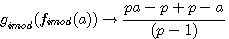
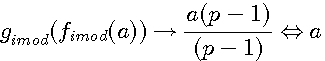


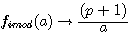 réalisons:
réalisons: 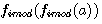
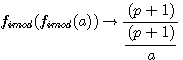
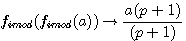
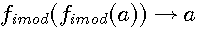

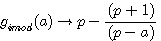 réalisons:
réalisons: