Les polygonaux 3D ou poly-polygonaux : Définition
|
Un nombre poly-polygonal est un entier représentant non pas un polygone (plat) mais un parallélépipède (volume) divisé en un certain nombre. Par exemple 4x5x6 / 6 = 20 est une pyramide de base triangulaire formée de 20 pierres. Il existe aussi des poly-polygonaux à base carré. |
Chapitre précédent : |
Les poly-polygonaux selon Pierre de Fermat
Sur l'étude du livre de Diophante "les nombres polygonaux" ,à la question : Étant donné un nombre polygonal trouver le coté, Fermat expose le théorème suivant :
Nous avons trouvé une belle et admirable proposition que nous placerons ici sans démonstration.
Dans la progression des nombres naturels commençant par l'unité, un nombre quelconque, multiplié par celui qui le suit et qui est plus grand, fait le double du triangulaire de ce nombre;
|
Ob(n)=
La multiplication du triangulaire, par le nombre qui le suit et qui est plus grand dans la progression, donne le triple du pyramidal; T(n)=
Le produit du pyramidal, par le nombre suivant de la progression, donne le quadruple du triangulo--triangulaire, Pt(n)
et ainsi à l'infini par une méthode générale et uniforme; et je ne pense pas qu'on puisse donner sur les nombres un théorème plus beau et plus général, je n'ai ni le loisir ni la convenance d'insérer la demonstration à la marge (1) |
Nombre triangulaire T(n)
T(n) =La somme de 1 à n Nombre Pyramidal Triangulaire=Pt(n)pyramide de base triangulaire
Pt(n)=La somme de la somme de 1 à n = Nbre Pyramidal Carré Pc(n) |
Ce que je traduit par: 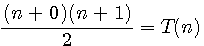 ;
;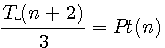 ;
;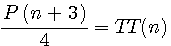
Qui
par déduction donne l'expression suivante : 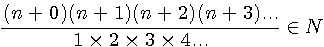
![]() On
retrouve dans les notes du 4 Novembre 1636 de Fermat à Roberval l'expression
suivante :
On
retrouve dans les notes du 4 Novembre 1636 de Fermat à Roberval l'expression
suivante : 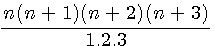 ,ce
qui est bien le quadruple du Triangulo-triangulaire , car divisé par 1.2.3 , et non pas 1.2.3.4
,ce
qui est bien le quadruple du Triangulo-triangulaire , car divisé par 1.2.3 , et non pas 1.2.3.4
![]() Cette formule est la base du petit théorème de Fermat
Cette formule est la base du petit théorème de Fermat
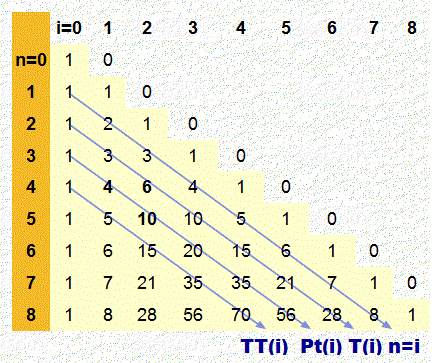
Matrice des nombres poly-polygonaux de base triangulaire: P3d(n,k)
|
P3d(n,k)=
|
Les lignes de ce tableau = n Les colonnes = k dans la formule ci-contre Exemple: N=4 k=3: Remarques:
1+4+10+20+35+56
-La somme de 2 triangulaires consécutifs étant égal à un carré alors:
Exemple Pt(7)-Pt(5) = 84-35=49=7²
|
Poly-polygonaux et relation de récurrence
Nous observons que l'élément suivant d'une colonne = l'élément de la même colonne + l' élément suivant de la colonne précédente, Exemple : TT(n+1)=TT(n)+Pt(n+1), si n= 3 (en rouge dans le tableau)=> TT(3+1)=35 = TT(3)=15+Pt(3+1)=20
Pour vérifier que cette conjecture est vrai ,calculons la différence entre un poly-polygonal(n+1) et le poly-polygonal(n) de la même colonne , c'est à dire du même type. Ce calcul implique que n >0 (u0=1)
Prouvons Pt(n+1)-Pt(n) |
||
|
Nota: 6=1*2*3=3!
|
exemple si n=5
Pt(6)=56 - Pt(5)=35 |
|
|
Factorisation des éléments communs du num. (n+1)(n+2) |
||
|
|
|
|
|
Suppression des parenthèses |
||
|
|
|
|
|
la différence de deux pyramidaux base triangulaire égale donc à : |
||
|
|
56-35=21 |
|
|
P3d(n+1, k)-P3d(n,k) Pour le calcul de la différence P3d(n+1,k) - P3d(n,k) , n>0 ,k>0 Si n est >0 alors k>1 donc k,n mini = k=1 ;
|
||
|
La séquence de k => k-1,k...k+1 ,la séquence totale du numérateur est du genre: (n+0)(n+1)....(n+(k-1))(n+k) |
exemple si n=7,k=4 = TT(7+1)-TT(7)
|
|
|
Factorisation des éléments communs du num. (n+1)(n+(k-1)) |
||
|
|
|
|
|
Suppression des parenthèses |
||
|
|
|
|
|
Suppression des parenthèses k/k! = 1/(k-1)=! |
||
|
|
|
|
|
||
Equivalence aux triangles de Pascal
Rappel sommaire
![]() Un nombre du triangle de Pascal est trouvé par la somme du contenu [n-1,i] + [n-1,i-1]
Un nombre du triangle de Pascal est trouvé par la somme du contenu [n-1,i] + [n-1,i-1]
![]() Une ligne n de ces nombre est aussi égale aux nombres trouvés dans un développement
Une ligne n de ces nombre est aussi égale aux nombres trouvés dans un développement
(x+y)n; Par exemple: (x+y)4 = 1x4 + 4x3y1 + 6x2y2 + 4x2y3 + 1y4
Tableau triangle de Pascal
|
Tableau des polygonaux 3d
|
Correspondance Triangle de Pascal et matrice des poly-polygonaux:
L'on constate une similitude très intéressante entre un triangle de Pascal et la table des poly-polygonaux de Pierre de Fermat.
à partir de 1654 Fermat et Pascal échangeaient bon nombres de correspondances principalement sur le "problème (statistique) des partis de jeux"
Divisibilité de n(n+1)(n+2)...
Pourquoi cette série est divisible par sa factorielle?
Dans la formule des cotés des polygones de Fermat, l'on constate que n(n+1)(n+2)... est toujours divisible par la factorielle du nombre de facteurs.
Par exemple la factorisation de 3 nombres consécutifs est toujours divisible par 6 (1x2x3 = factorielle 3), de 4 nombres consécutifs est toujours divisible par 24 (4!)...
Cette propriété est la base du Petit théorème de Fermat
Nombres de nombres divisibles et nombres premiers:
|
Divisible par 2 (en gras) |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
|
Divisible par 3 (en gras) |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
15 |
16 |
Dans la ligne Divisible par 2, un nombre sur 2 est divisible par 2.
Dans la ligne Divisible par 3, un nombre sur 3 est divisible par 3.
Si dans une série de 3 nombres , cette série contient 2 nombres premiers alors obligatoirement le 3ème nombre est forcement divisible par 6
Exemple 11,12,13 , 12 est le nombre non premier divisible par 6.
Vidéos  sur les polygonaux et polygonaux 3d
sur les polygonaux et polygonaux 3d
1er Partie
2 éme PartieLes poly-polygonaux à base carré |
source:Oeuvres mathématiques et de l'arithmétique de diophante par E.Brassine (XIX éme siècle) aux éditions Jacques Gabay

Patrick Stoltz le 19/02/2009 – MAJ le 8/07/2010-13/01/2015 - 25/08/2019 - 08/03/2021

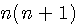 = 2T(n) =
= 2T(n) = 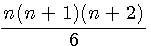
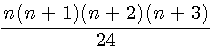 ]
]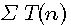

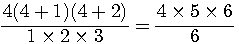 =20
=20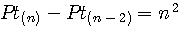
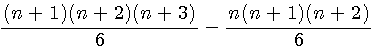
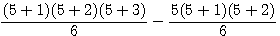
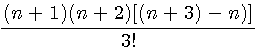
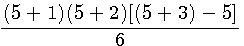
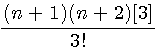
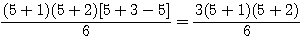
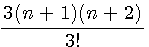 =
=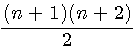 =T(n+1)
=T(n+1)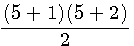 =T(5+1)=21
=T(5+1)=21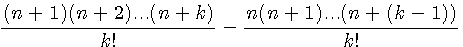
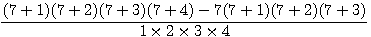
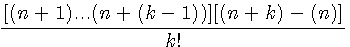
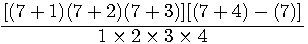
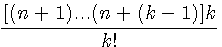
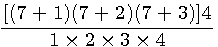
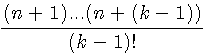 =P3d(n+1, k-1)
=P3d(n+1, k-1)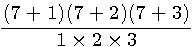 =Pt(N+1)
=Pt(N+1)