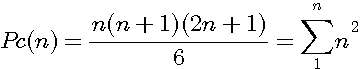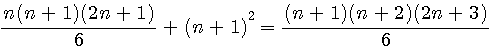
Définition
|
Un nombre poly-polygonal à base carré est un entier représentant non pas un nombre polygonal plat extrapolé à partir d'un nombre triangulaire, mais un parallélépipède (volume) à partir d'un triangulaire carré. Par exemple 4x5x9 / 6 = 30 est une pyramide de base carré formée de 30 pierres, en fait = à 1²+2²+3²+4² (1+4+9+16 = 30) |
Chapitre précédent :
|
Rappel d'un nombre triangulaire et triangulaire carré
Un nombre triangulaire T(n) est le produit de deux nombres entiers consécutifs divisé par 2
Il s'exprime sous la f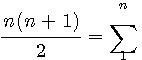orme :
Un nombre triangulaire CARRE TC(n) est un nombre polygonal de base carré.TC(n) est la nième somme de nombres impairs ; Il s'exprime ,selon Pierre de Fermat
(*), sous la forme :
(*) 
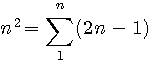ou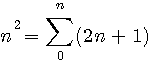 
Les nombres polygonaux étant la représentation d'un polygone à partir d'un triangle, je n'aborderai un poly-polygonal à base carré qu'à la 3ème dimension c'est à dire une pyramide.
Pyramide à base carré , trouver la formule
TC(n) = T(n-1)+T(n) ;Un Triangulaire carré étant la somme d'un triangulaire de rang inférieur n-1 + un triangulaire de rang n.
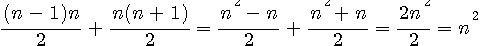
Nous posons donc un pyramidal carré Pc(n) = un pyramidal Pt(n) + un pyramidal de rang inférieur Pt(n-1) :
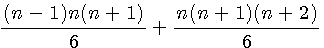
Factorisation du numérateur par n(n+1) => n(n+1)[n-1 + n+2]/6 =>
|
|
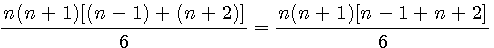
Pyramide à base carré : Pc(n).Démonstration de la relation de récurrence
On trouve, sur l'étude de terminale S sur les relations de récurrence,un exercice pour prouver que cette formule est bien la somme des carrés de n ; Je vous propose la même démonstration sans tout développer et refactoriser , ce qui est très fastidieux et source d'erreurs.
Il s'agit donc de prouver que Pc(n)+(n+1)²+Pc(n+1)
Trouver la valeur de Pc(n+1)
Soit n(n+1)(2n+1)/6 si je remplace n par (n+1) alors Pc(n+1)= (n+1)(n+2)(2(n+1)+1)/6 = (n+1)(n+2)(2n+3)/6
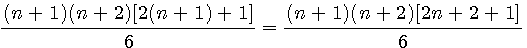
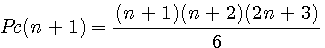
Prouver que Pc(n)+(n+1)²=Pc(n+1)
il suffit de séparer le tout en 2 :
Séparer le pyramidal carré en la somme du pyramidal Pt(n-1) et le pyramidal de Pt(n) , comme vu précédemment
Séparer le carré de rang supérieur (n+1)² en 2 triangulaires , T(n) + T(n+1)=(n+1)²
Pc(n)+(n+1)²=Pt(n-1)+Pt(n)+T(n)+T(n+1)
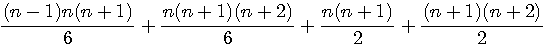
Les 2 triangulaires au même dénominateurs: T(n)=3T(n)/3 , T(n+1)=3T(n+1)/3
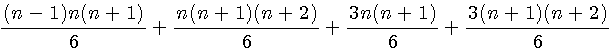
Pt(n-1)+3T(n)/3 + Pt(n)+3T(n+1)/3
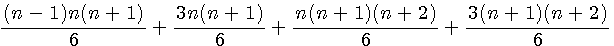
Factorisation des 2 premiers termes par n(n+1) , des 2 derniers termes par (n+1)(n+2)
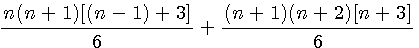
Simplification
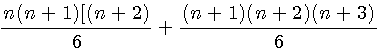
Factorisation des 2 termes par (n+1)(n+2)
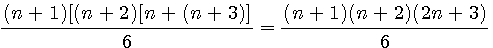
donc
|
|
Vidéos 
sur les polygonaux et polygonaux 3d
2ème Partie
source:Oeuvres mathématiques et de l'arithmétique de diophante par E.Brassine (XIX éme siècle) aux éditions Jacques Gabay
Patrick Stoltz le 19/02/2009 – MAJ le 8/07/2010-13/01/2015 - 25/08/2019 - 08/03/2021