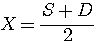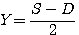Dans le tutoriel Somme=S et Différence=D de 2 nombres x et y nous avons développé S+D (voir ci dessous) mais aussi :

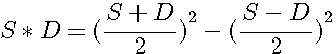= X²-Y²

(S*D)² ou Somme² x Différence²

Si du point de vue mathématique (ab)² = a²b² , (SD)² ou S²*D² peut être exprimé de 2 façons pour le même résultat :

(SD)²

Puisque SD = X²-Y² alors (SD)² = (X²-Y²)²

Exemple : (7*3)² => x=5 y=2 =>(5²-2²)² = 21²

Dans l'expression :

si je remplace S par s² et D par d² alors:

par exemple S=49 D=9 =>S=7² et D=3²

S est une somme : X + Y

D est une différence : X-Y

S=(x+y) et D=(x-y)

S+D=(x+y)+(x-y)

S-D=(x+y)-(x-y)

S+D=x+y+x-y

+y-y=0

S+D=2x

S-D=x+y-x+y

x-x=0

S-D=2y

exemple 7²*3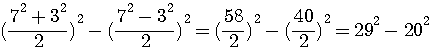² = = 21²

nota: 29²=20²+21² est un triplet pythagoricien

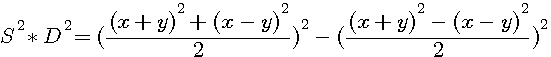
(x+y)²+(x-y)²=x²+2xy+y²+x²-2xy+y²

S²+D² = 2x²+2y²

S²+D² = 2Z

(x+y)²-(x-y)²=x²+2xy+y²-[x²-2xy+y²]

(x+y)²-(x-y)²=x²+2xy+y²-x²+2xy-y²

S²-D²=2x²2y² = 4x²y²

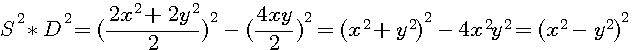=(SD)² = (X²-Y²)²

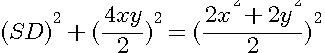
Ce qui aboutit à l'équation de Diophante et Pierre de Fermat ,abondamment utilisée pour les triangles rectangles :

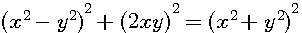
suite :