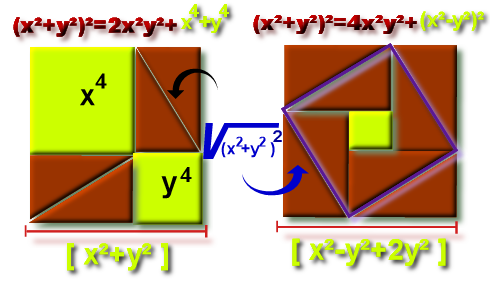
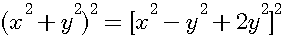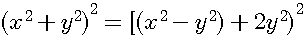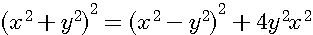L'équation de Diophante (x²-y²)² + 4x²y² = (x²+y²)²
Dans le Livre III question 22 , Livre V question 8 ... Pierre de Fermat utilise sans cesse cette équation qui est la base des triangles dit rectangle.
Pour rappel : Z = X²+Y² est un carré dont la surface est un entier mais son coté est un réél qui n'existe pas dans le monde de Fermat et encore moins Diophante (voir ci-contre)
Exemple 2²+5² = 29 , le coté de ce carré mesure
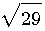, = hypoténuse d'un triangle quelconque
Par contre Z²=(x²+y²)² , sa surface sera toujours un entier et son coté = x²+y² sera aussi un entier = hypothénuse d'un triangle rectangle
Exemple 3²+4² = 25 son coté mesure
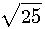= 5 = 2²+1² : Z²=(2²+1²)² => Z= 2²+1²
La formule générale sans cesse employée par Diophante est : (x²+y²)² = (x²-y²)²+(2xy)²
Hypoténuse d'un triangle dit quelconque
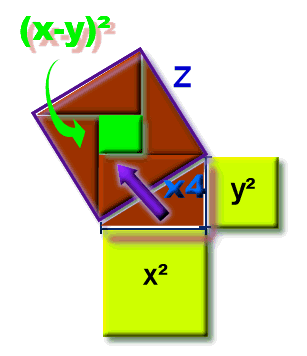
Cette formule permet de "générer" n'importe quelle hypoténuse entière.
Ci-contre une hypothénuse d'un triangle rectangle du point de vue de la longueur de l'hypothénuse
Exemple: 
Prenons x=3 y = 2 => (3²-2²)² + (2*3*2)² = (3²+2²)² , c'est a dire 5²+12²=13²
Vérification:
Hypoténuse d'un triange dit rectangle
=
=
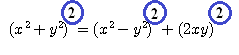
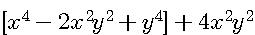
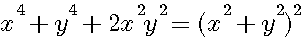
nota
(x²-y²)² = (x-y)(x+y)²
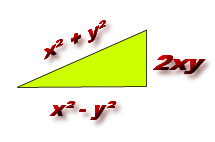
Démonstration de cette formule par les surfaces équivalentes
|
|
Dans sa descente infinie , Fermat pose une autre égalité equivalente visualisée ci-contre:
parenthèses sur x²-y²
|
=
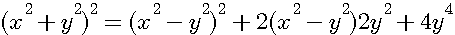
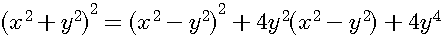
multiplication de 4y²par (x²-y²)
=
|
|
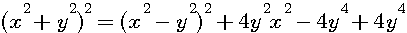
