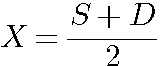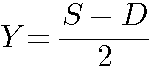Une des bases de l'étude des nombres de l'Arithmética de Diophante (question 30 du livre 1) est la somme et la difference de 2 nombres  , la somme et la différence de 2 carrés etc etc...

Somme et différence de deux nombres

Exemple : 13 est une somme de 2 nombres S  ; 3 est une difference de 2 nombres D

X=(13+3)/2 = 8 : Y=(13-3)/2 = 5

vérification:

S=X+Y=8+5 = 13 , D=X-Y = 8-5=3

Autre exemple 15 est une somme S ; 6 est une différence D

S=15 et D = 6 : X = 21/2 et Y = 9/2 , S=X+Y = 21/2+9/2 = 30/2 = 15 , D=X-Y = 21/2-9/2 = 12*2 = 6

SxD=(x+y)(x-y)

Soit SxD = (x+y)(x-y) = x²-y²; x=(S+D)/2 et y = (S-D)/2

par exemple (7)(3)=21 ; x=(7+3)/2 = 5 ; y = (7-3)/2 =>

7*3 = (5+2)(5-2)=5²-2²=21

SxD =(x+y)(x-y) = x²-y² pour trouver la valeur de x nous devons appliquer x=(S+D)/2 et y = (S-D)/2 donc:

Rappel

a²-b²=(a+b)(a-b)

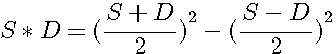=> SD=X²-Y²

Nous notons aussi que:

Donc Y est toujours plus petit que X ; SD = X²-Y² et Y²< X²

Et aussi

Exemple N=90 =  S=15 et D = 6  : X = (21/2)² - (Y = 9/2)²  

SD + Y² = X²

Puisque SxD = (x+y)(x-y) = x²-y² (et que y<x) donc SxD = (x+y)(x-y) + y² = x²

Exemple : 5 = SD = 5*1 , y sera égal à 2 c'est à dire (5-1)/2 d'où l'on déduit que 5*1 + 2² = 3²

Nous pouvons vérifier que x = (S+D)/2 = (5+1)/2 = 3

Autre exemple : SxD = 5*2 => y=(5-2)/2 = 3/2 => S*D=10 + (3/2)² = 7²/2² est un carré x²

Nous pouvons vérifier que x = (S+D)/2 = (5+2)/2 = 7/2 ; S=x+y = 7/2+3/2 = 5 D= 7/2-3/2=2

SD + 2Y² = X²+Y²=Z

Puisque SxD = (x+y)(x-y) = x²-y² donc SxD = (x+y)(x-y) + 2y² = x²+y²

Exemple   : 5 = SD = 5*1 , 5*1 + 2*2² = 3²+2²=13

Exemple   : 21 = SD = 3*7 = y sera égal à 2 c'est à dire (7-3)/2 d'où l'on déduit que 3*7 + 2*2² = 5²+2² = 29

Rappel : Z est une somme de deux carrés dont l'hypoténuse =

Divisibilité de SD

S et D non divisible par 3

Soit SD = (X+Y)(X-Y) =X²-Y² si S et D non divisible par 3 alors X ou Y sera divisible par 3

Démonstration:

Soit N un nombre entier alors je peux l'exprimer sous la forme 3n , 3n+1 ou 3n+2  ; Exemple : 7 = 3(2)+1

Que signifie :

 N 0 (mod p)

Si nous divisons N par p le reste de la division EUCLIDIENNE est 0

exemples:

le reste de 12 / 3 = 0 ,

sera noté : 12 0 (mod 3)

le reste de 11 / 3 = 2 ,

sera noté : 11 2 (mod 3)

(9+2=11)

ou 11 -1 (mod 3)

(11=12-1)

Dans l'arithmétique modu-laire seul le reste compte

Plus de précisions sur:

S et D divisible par 3 :

Si S et D est divisible par 3 alors il existe FORCEMENT un autre produit où S ou D n'est pas divisible par 3

soit 3x*3y = 3*3*x*y = 3²xy que l'on peut étendre à : 3^ax*3^by = 3^(a+b)xy => 3^(a+b)x 0 (mod 3)

S ou D divisible par 3 :

Si S ou D divisible par 3 alors 2x=(S+D) ET 2y=(S-D) seront NON DIVISIBLE PAR 3

Si 3(a)[3(b)+1] ou 3(a)[3(b)+2] alors 2x= 3(a)+[3(b)+1] ou 3(a) + [3(b)+2] et 2y =  3(a)-[3(b)+1] ou 3(a) - [3(b)+2]    (voir exemples ci-dessus)

2x2y = S²-D² =(S+D)(S-D)

Dans ce chapitre nous traitons de l'inverse de 4SD=x²-y² C.A.D 4xy = S²-D²

Dans le Livre I question 30 , Diophante utilise l'équation: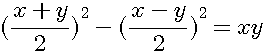     

qui est aussi égale à : 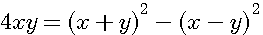  = S²-D² que l'on peut énoncer par:

Rappel : (S+D)=2x et (S-D)=2y donc (S+D)(S-D)=2x*2y

Vérification:

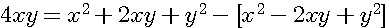
suppression de la parenthèse

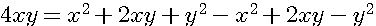
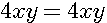
Détails:

Vidéo sur le sujet :