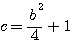Oblong numbers
The product of two consecutive integers expresses himself under the shape 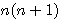 ou
ou 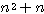 .
.
It's "Diophantesque equation" base
Triangulars numbers
N-th triangular number is equal to sum of N firsrt integers not nul
example for n=4 , 1+2+3+4 = 10
It's also an oblong number / 2
|
Others Formulae :
A number raised to the square - this number = among lower rank in the square increased by this number less a unit |
Maybe base of Fermat's small theorem ...
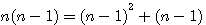
n=5 : 5(5-1)=(5-1)²+4=20
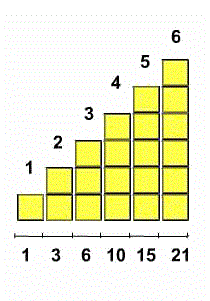
Glossary:
Rank: position un the sum (6 is at rank 3)
Altitude : high of rank (3 in third rank) in this case = n
This one (Altitude) to use among others in the guess of Syracuse; it's not used by Fermat what makes very difficult its translation
T = Triangular
ST= Squared Triangular
P=Pyramidal
SP =Squared Pyramidal
ST : squared triangular
Squared triangulars numbers animated of powered numbers: an altitude "fold" to form a new square
Sum of 2 consecutives odd numbers
It's also the sum of 2 triangulars - n
example : 6+6-3 = 3²
Important an Altitude equal a 'A' in Even topologic squares
If a root of an altitude is an interger then we produce a right angled triangle
Severals formulae
A=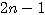
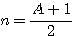
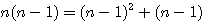
| n | 2n-1 (A) | ST (n²) | (A+1)/2 |
| 1 | 1 | 1 | 1 |
| 2 | 3 | 4 | 2 |
| 3 | 5 | 8 | 3 |
| 4 | 7 | 12 | 4 |
| 5 | 9 | 16 | 5 |
| 6 | 11 | 20 | 6 |
| 7 | 13 | 24 | 7 |
| 8 | 15 | 28 | 8 |
| 9 | 17 | 32 | 9 |
| 10 | 19 | 36 | 10 |
| 11 | 21 | 40 | 11 |
| 12 | 23 | 44 | 12 |
| 13 | 25 | 48 | 13 |
| 14 | 27 | 52 | 14 |
| 15 | 29 | 56 | 15 |
TC=sum A until n rank
"Pliage" d'altitude
Polygonals numbers from Fermat
Observation of Fermat on Diophante's problem study: Find the side of a polygonal
Nous avons trouvé une belle et admirable proposition que nous placerons ici sans démonstration.
Dans la progression des nombres naturels commençant par l'unité, un nombre quelconque, multiplié par celui qui le suit et qui est plus grand, fait le double du triangulaire de ce nombre;
La multiplication du triangulaire, par le nombre qui le suit et qui est plus grand dans la progression, donne le triple du pyramidal;
Le produit du pyramidal, par le nombre suivant de la progression, donne le quadruple du triangulo--triangulaire, et ainsi à l'infini par une méthode générale et uniforme; et je ne pense pas qu'on puisse donner sur les nombres un théorème plus beau et plus général, je n'ai ni le loisir ni la convenance d'insérer la demonstration à la marge
source:Oeuvres mathématiques et de l'arithmétique de diophante par E.Brassine aux éditions Jacques Gabay
We found beautiful and admirable one proposition which we shall place here without demonstration.
In the progress of the natural numbers beginning with the unity(unit), some number, multiplied by the one who follows him(it) and who is bigger, made the double(copy) of the triangular of this number;
The reproduction of the triangular, by the number which follows him(it) and which is bigger in the progress, gives the triple of the pyramidal;
The product of the pyramidal, by the number following by the progress, gives the quadruple of the triangulo - triangular, and so in the infinity by a general and uniform method; and I do not think that we can give onto the numbers more beautiful and more general theorem, I have neither the leisure nor the suitability to insert the demonstration marginally
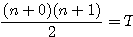 ;
; 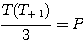 :
: 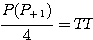
Witch with translating give me:
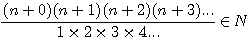
We found in Fermat's correspondance to Roberval du 4 Novembre 1636 , the 4th November the following
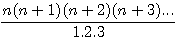
It's the fouth quantity fo the following
Squared triangulars numbers and topologic squares guess
Odd Topology |
|||
|
An Altitude of 9 forms a square of 5 - a square of 4 (in white) according to the principle of an odd topological square |
For a right angled triangle noted a,b et c his hypothénuse, A is a TC's altitude.
|
||
Even Topology (b even) |
|||
|
An even square consists of 2 AltitudesThese 2 altitudes recompose a new square according to the model " squared even ". |
|
||

Patrick Stoltz le 19/02/2009 – upgrated in 07/08/2010
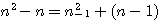
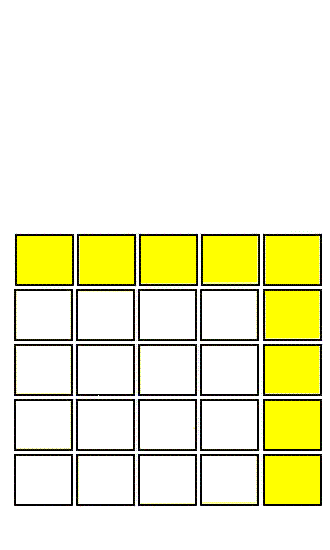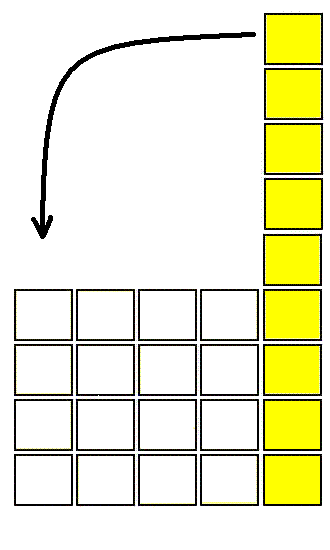
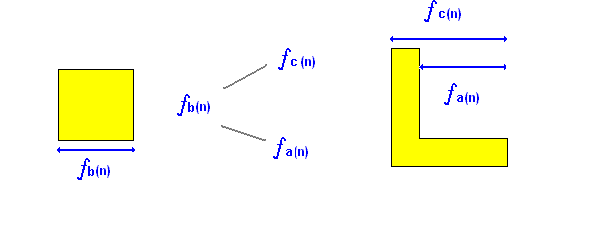
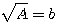
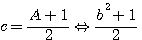 = formulae of
= formulae of 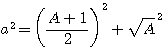
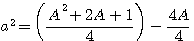
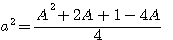
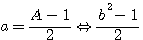 = formulae of odd topologie for a
= formulae of odd topologie for a
 =
= 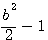 ,
,  =
= 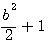
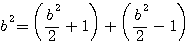
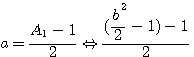
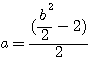 =
=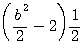
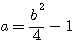 =
= 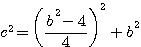
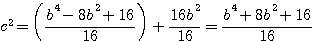
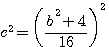 ,
,