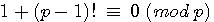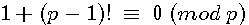|
|
 |
Tweet to @schemath |
Fermat's little theorem (condensed):
In mathematics, the Fermat's little theorem is a result of the modular arithmetic, which can also demonstrate itself with the tools of the elementary arithmetic.
It expresses itself as follows. If 'a' is a not divisible integer by p such as p is a prime number, then a p-1 -1 is a multiple of p. The corollary of this theorem is that, for every 'a' interger and 'p' prime number, then ap -1 is a multiple of p.
He owes his name to Pierre de Fermat (on 1601 - 1665) who expresses it the first time on October 18th, 1640.
|
We can read that |
what mean
It's mean that if I divide n by p the rest of this division is 0 example: the rest of 12 / 4 = 0 , it will be noted :
|
the Fermat's poly polygonals "key" formula
|
If we use the Pierre de Fermat's poly-polygonals formula : |
Notation n! = Factorielle n instead of 1x2x3x4... n , we write n! 1x2x3x4 = 4! = à 24 |
Example for 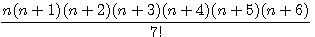 =
= 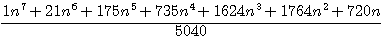
Fermat has proved all his theories (little ,and last theorem) for all power of n , so it is absolutely excluded that Fermat have built them by EACH indices on n. example for 7! indices are 1,21,175,735,1634,1764,720 (see before) . But we can , with a small trick, found the sum off all of them.
How to find the sum of all indices ?
If 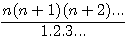 ,we shift n by 1 (n=1) then we get
,we shift n by 1 (n=1) then we get 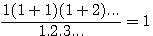
|
|
If we develop n(n+1)(n+2)...(n+p) , the sum of all indices is equal of the factorial of denominator , example for 7! , 1+21+175+735+1634+1764+720 = 5040
Development of numerator:
if p numbers of factors of n(n+1)(n+2).. then
|
.
=
|
![]() The FIRST exponent = numbers of factors (as Pascal's board), 1p
The FIRST exponent = numbers of factors (as Pascal's board), 1p
![]() The FIRST indice is equal to 1
The FIRST indice is equal to 1
![]() The LAST indice = factorial -1 of numbers of factors.
The LAST indice = factorial -1 of numbers of factors.
Exemple : nombre de facteurs = 7
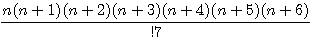 <=>
<=> 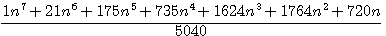
![]() The FIRST exponent = numbers of factors : 1n7
The FIRST exponent = numbers of factors : 1n7
![]() The FIRST indice is equal to 1 , 1+21+175+735+1624+1764+720=5040
The FIRST indice is equal to 1 , 1+21+175+735+1624+1764+720=5040
![]() The LAST indice = factorial -1 of numbers of factors.1+21+175+735+1624+1764+720=5040 , 1 x 2 x 3 x 4 x 5 x 6 =720
The LAST indice = factorial -1 of numbers of factors.1+21+175+735+1624+1764+720=5040 , 1 x 2 x 3 x 4 x 5 x 6 =720
Shifting n by 1
|
if n = 1
|
For example for 7 factors
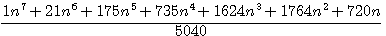 if n = 1 then
if n = 1 then 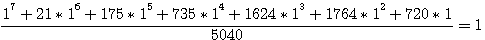 ,
,
1+21+175+735+1624+1764+720=5040 = 7!
Demonstration of Fermat's small theorem
Primaries numbers and factotials
If a number is primary , understand divisible only by himself or 1 , imply that only that the last factor of his factorial is divisible by this number , by example , 7 is primary so 7! = 1 x 2 x 3 x 4 x 5 x 6 x 7 only the last factor , 7 , is divisible by 7 , and NOT the others 2,3,4,5,6 (we get a NOT INTEGER one , we get a decimal number or real )
We deduct also that if a number is primary his factorial LESS ONE is not divisible by this number 2 x 3 x 4 x 5 x 6 is not divisible by 7.
|
Terms of adding indices and primaries:
If [1+ (a+b+c) ] + [(p-1)! ] is divisible by p equal also : [1] + [a+b+c]+ [(p-1)!]
Concatenation (grouping) in 2 terms
We regroup all the terms of 1+...+ (p-1)! .... in 2 terms :
We concatenate 1 + a + b+ c ...and we add the last term (p-1)! |
|||||||||||||
|
Example : n(n+1)(n+2)(n+3)(n+4) , if n=1 then we get 1(1+1)(1+2)(1+3)(1+4) ; sum of all indices 5! = 120 , last indice = 4! =24 then 120 = 96+24 note that if we factorise the twice terms by 24 then 120 = 24(4+1)
120=4x24 + 1x 24 , first = 4x4x3x2x1 , last = 4x3x2x1 That still true for promary numbers of factors or not
|
n(n+1)...(n+p-1)=n^(p-1)+..(p-1)n ,p in numbers of factors
Nota:development of n(n+1)(n+2)(n+3)(n+4) = 1n5+10n4+35n3+50n2+24n |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Concatenation in 3 terms , first / intermediate / last
P! is a sum of p terms which the first equal to 1 and the last one = (p-1)! , We add all intermediate terms in a second term =
p!-1-(p-1)! = p!-(1+(p-1)!) so 120 = 1 + [120-(1+24)] + 24 = 1 + 95 + 24
The second term is divisible by p (as show bellow) , so we can discard it..
If p is primary , then (p-1)! is not divisible by p , 1 is not divisible by p , 1+ [p!-(1+(p-1)!)] + (p-1)! is divisible by p
<=>
If [1] + [p!-(1+(p-1)!] + [(p-1)!] , ![]() 0 (mod p) , 1+(p-1)! is divisible par p .
0 (mod p) , 1+(p-1)! is divisible par p .
More details
|
p! = ( p=5 => 1x2x3x4x5=120) |
|||||
|
|
|||||
|
1st + 2nd terms |
+ |
Last term |
|||
|
(p-1)(p-1)! (5-1)(5-1)(5-2)(5-3)(5-4) = 4x4x3x2x1 = 96 4x4x3x2x1 not divisible by 5 |
+ |
(p-1)! 4x3x2x1 = 24 4x3x2x1 not divisible by 5 |
|||
|
|
|
||||
|
1st = 1 |
+ |
+ 2nd terms |
+ |
Last term |
|
|
1 |
+ |
p! - 1 - (p-1)! = p! - (1+(p-1)!) 120-1-24= 120 - (25) = 95 |
+ |
+ (p-1)! |
|
|
1 |
+ |
p! - |
1+(p-1)! |
+ |
+ (p-1)! |
|
|
|
= le premier + dernier terme |
|
|
|
|
p! Those 2 terms are equals so |
|||||
|
Conclusion:
In Fermat's poly-polygonals formula , n(n+1)(n+2)...(n+(p-1)) , if p numbers of factors and if we shift n by 1 then : If p is primary , 1 + 1*2*3...(p-1) is divisible by p
|
n n
You can see this item |
|
|
For example p=7 then 1+1*2*3*4*5*6 = 721 divisible by 7
Replace now 1 by n = get the Fermat's small theorem
If n(n+1)(n+2)...(n+p-1) = [1np]+[anp-1+bnp-2]+[(p-1)!n] then
|
If 1+(p-1)! n+n(p-1)! et aussi : n+n(p-1)! |
In the last term of 1n5+10n4+35n3+50n2+24n , 24n + n = 25n is divisible by 5 , so the first - n is divisible by 5 , it means that if we adding n to the last term for make it divisible we have to subtract n to the fisrt ( np -n)
|
si n+n(p-1)! |
Prime number's guess in corollary of Fermat's small theorem
 n is
prime if
n is
prime if  (or
(or  )
)
Shoud redable as following : if the reminder of 2n-2 / n is 0 <=> if the reminder of 2n-1-1 /n est 0
Ensuing of Fermat's small theorem,if a=2; if remainder (= modulo 1) of a n-a/a = 0 then n is prime number (if not n is not prime)
It's only a guess because it's necessary to be able to demonstrate it (*),2 n Exceeds the capacities of calculations and calculators...
(I'm writing modulo 1 because it's the computer function
, should be  )
)
It's very important to see that in this guess only 2n put numbers into 2 well separed groups , primes and non primes

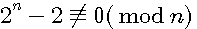
(*) Professor Henry Cohen of the university of Bordeaux notes " We can conclude nothing if 2n-1 1 is divisible by n, but it is rather likely in this case that n is prime (Number's history Tallandier Edition 2007)
This conjecture is not true for (n< 1000) 341,561,645 !!!:
Comments
Matrice showing this guess (a=2)
Fermat small theorem don's separate prime and not prime as well as wish.:
Samples :
a=3 n=6 , 6 is not prime , the 36-3/3 reminder should be <> 0
nb: 3 as 2 is prime...
|
n |
36 |
36-3 |
726/6 |
Rem |
| 6 | 729 | 726 | 121 | 0 |
pour a=5 , n=10
| n | 510 | 510 -5 | 510 -5/5 | Rem |
| 10 | 9765625 | 9765620 | 976562 | 0 |
It's seems to be the same for all n/a = 2 ...
For a= 4 it's worse...
| n | 4n | 4n-4 | 4n-4/4 | r |
| 2 | 16 | 12 | 6 | 0 |
| 3 | 64 | 60 | 20 | 0 |
| 4 | 256 | 252 | 63 | 0 |
| 5 | 1024 | 1020 | 204 | 0 |
| 6 | 4096 | 4092 | 682 | 0 |
| 7 | 16384 | 16380 | 2340 | 0 |
Small appended notes:
If we want to know if a number is divisible by other one of head you should:
If it's even divide it by 2
If it's odd substract it : "lui ôter une mesure"as would have written it Fermat....)
Ensue of binary algorithm
.
| n | 2n | 2n – 2 | 2n – 2 / n | mod |
|
1 |
2 |
0 |
0 |
0 |
|
2 |
4 |
2 |
1 |
0 |
|
3 |
8 |
6 |
2 |
0 |
|
4 |
16 |
14 |
3 1/2 |
1/2 |
|
5 |
32 |
30 |
6 |
0 |
|
6 |
64 |
62 |
10 1/3 |
1/3 |
|
7 |
128 |
126 |
18 |
0 |
|
8 |
256 |
254 |
31 3/4 |
3/4 |
|
9 |
512 |
510 |
56 2/3 |
2/3 |
|
10 |
1024 |
1022 |
102 1/5 |
1/5 |
|
11 |
2048 |
2046 |
186 |
0 |
|
12 |
4096 |
4094 |
341 1/6 |
1/6 |
|
13 |
8192 |
8190 |
630 |
0 |
|
14 |
16384 |
16382 |
1170 1/7 |
1/7 |
|
15 |
32768 |
32766 |
2184 2/5 |
2/5 |
|
16 |
65536 |
65534 |
4095 7/8 |
7/8 |
|
17 |
131072 |
131070 |
7710 |
0 |
|
18 |
262144 |
262142 |
14563 4/9 |
4/9 |
|
19 |
524288 |
524286 |
27594 |
0 |
|
20 |
1048576 |
1048574 |
52428 5/7 |
5/7 |
|
21 |
2097152 |
2097150 |
99864 2/7 |
2/7 |
|
22 |
4194304 |
4194302 |
190650 1/9 |
1/9 |
|
23 |
8388608 |
8388606 |
364722 |
0 |
|
24 |
16777216 |
16777214 |
699050 4/7 |
4/7 |
|
25 |
33554432 |
33554430 |
1342177 1/5 |
1/5 |
|
26 |
67108864 |
67108862 |
2581110 1/9 |
1/9 |
|
27 |
134217728 |
134217726 |
4971026 8/9 |
8/9 |
|
28 |
268435456 |
268435454 |
9586980 1/2 |
1/2 |
|
29 |
536870912 |
536870910 |
18512790 |
0 |
|
30 |
1073741824 |
1073741822 |
35791394 1/9 |
1/9 |
|
31 |
2147483648 |
2147483646 |
69273666 |
0 |
|
32 |
4294967296 |
4294967294 |
134217727 8/9 |
8/9 |
|
33 |
8589934592 |
8589934590 |
260301048 1/6 |
1/6 |
|
34 |
17179869184 |
17179869182 |
505290270 1/9 |
1/9 |
|
35 |
34359738368 |
34359738366 |
981706810 4/9 |
4/9 |
|
36 |
68719476736 |
68719476734 |
1908874353 5/7 |
5/7 |
|
37 |
137438953472 |
137438953470 |
3714566310 |
0 |
If mod = 0 then n is prime ... if not n is not
Important notice
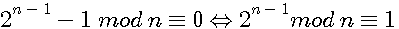
by add one on two sides
Is 221 dividable by 7?
221-7=214
214/2=107
107-7=100
50/2=27
27-7=20
20/2=10
10/2=5
221 n'est pas divisible par 7
(31*7 reste 4)
Is 91 dividable by 7?
91-7=84
84/2=42
42/2=21
21-7=14
14-7=7
.

Patrick Stoltz le 18/10/2009

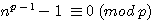
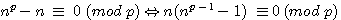 , but , if n is divisible by p ,
, but , if n is divisible by p , 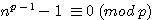
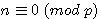 ?
?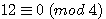
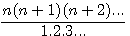 and we develop the numerator, then we have a formula like this:
and we develop the numerator, then we have a formula like this: 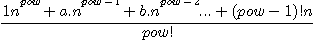 (pow mean powered by)
(pow mean powered by)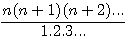 if n=1 then
if n=1 then 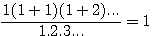
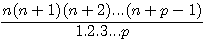
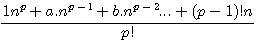
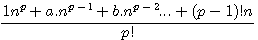
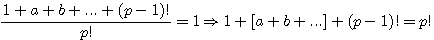
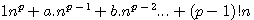 from the development of n(n+1)(n+2).... whose p ,numbers of factors, is primary and where we remplace n by 1
from the development of n(n+1)(n+2).... whose p ,numbers of factors, is primary and where we remplace n by 1