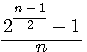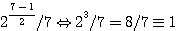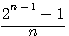During this study, I try to visualize prime numbers, their distributions and the means of reduire major powers of 2...To do it, I use the topology of formed squares (according to the same as topologic squares principle) to refine / counter this guess.
2n even and odd
Square topology formed by 2n are different according if n even or odd (Always and still)
To obtain an even root from even square (in binary for example) you can divide power by 2
28 = a square of 24 * 24 , 256 is a square of 16*16
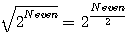
On the other hand for a 2 odd you should divide this number by 2 (or apply 2 n-1), then form a rectangle composed by 2 even squares witch the smallest ridge is the root of the even square, and the big one 2 * the root of even square
Example: 25 = a rectangle of 2 (5-1)/2 * 2(2 (5-1)/2) or (2 (5+1)/2)
25 = 22 * 23 , 32 is a rectangle of 4 * 8
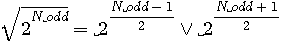 (V signify OR), will be explained following
(V signify OR), will be explained following
Graphing 2n fly
This animation demonstrate also the Fermat's two square guess
Guess : is 2 n-1 -1 / n mod 1 =0 is prime / Graphing Fermat's two squares guess
|
|
By definition a prime numbers is odd , except 2, there are in very precise group. As showed by Riemann, odd numbers are in 1/2 + it axis, (even numbers in négative axis) If n is always odd, n-1 is thus a power always even.If apply Then we divide by n for know if mod = 0 and if it's prime or not
This guess demonstrate also the Fermat's two square guess: all primes divided by 4 is modulo 1 To the left : This 24 square have a side of 22 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
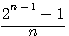 (for n odd), all primes numbers are drawing by a 2
(for n odd), all primes numbers are drawing by a 2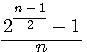
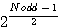
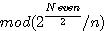
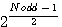 = root
= root 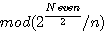 = remaining of square / n
= remaining of square / n