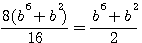Is Fermat a liar ?
By crossing a lot of mathematicians' books, all agree to think that Fermat assertion " I found a wonderful demonstration of this proposition, but the margin is too narrow to contain her(it) " without having to find the solution; we think that he had found for the powers of 3 , maybee 4 but no more.
In my mind I think Fermat had found a logical solution (more than mathematical because it is evident that matematics tools which have allowed of STW's and Whiles's formulaes did not exist), hardly probably by the etude of the differences of his polygonals numbers: 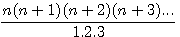
Also by examining the drawings of Fermat, he studied the topology of triangles topology, not squares as me.
The fact we can take in reference the model of the multidimentional representation which was visible to the "Palais de la Découverte , Paris" ; This model was a volume of a combination of triangles
I've looking by this way but I've not found; but on this guess I prupose an other simpliest solution to demonstrate that it's possible to found with the Fermat's and Diophante arithmetics
Certainly my approach is more logical than mathematical (I am a computer specialist of job, with a very few knowledge in mathematics), I even read that in topologic's terms , mathematicians don't like cutting objects (which Euler is the founding father).
Below you will also find the formulae of cuts of volumes.
Odd topologic reminder
Odd topology
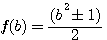 : This formulae allows calculation of C and A in C²=B²+A² : It is especially necessary to considerer B²=C²-A²
: This formulae allows calculation of C and A in C²=B²+A² : It is especially necessary to considerer B²=C²-A²
nota: I've put aside k...for the moment (common to A,B,C)
Sample: 3²=5²-4² ; B=3
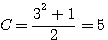 ,
,
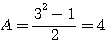
The big originality of this formula is the obtaining of 2 parameters (c and a) with only one parameter ( b )
Simpliest solution : General idea
Look on this formulae, numbers (3,4,5 in the sample) are powered by one, for pour l'utiliser you nead to power each term by 2. B*B=C*C-A*A ; 3*3 = 5*5 - 4*4 ; 9=25-16
|
C²= C²= |
A² = A² = |
|
x² (=b²)=C²-A²
C²-A² = B² |
|
The general idea is to continue the factorization of f( b ) and to study differences
Because with the odd and even squares formulae 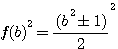 ,we produce in logic an infinity of right-angled triangles (with a single parameter), i continue by factorizing by the same logical way
,we produce in logic an infinity of right-angled triangles (with a single parameter), i continue by factorizing by the same logical way
If f+(3)² = 25 et f-(3)² = 16 (Odd topo) then his LOGICAL cube is f+(3)3=125 et f-(3)3=64
Topologic volumes - Looking divisor
Cutting a cube by 3 , 3 ridges missing + 1
Topologics volumes: extrapolation V-R
n |
Form |
Nb Vertexs / Ridges n(2n-1) |
|
0 |
20 = one point | 1:... |
|
1 |
21 = Draw |
2 : Basic Topologic square . 2 Vertexs , Maybe 2 Ridges because no faces? |
|
2 |
22 = un carré |
4 : 4 V , 4 R. Divisor as showed to the left |
|
3 |
23 = un cube |
8 : 8 V , 12 R. |
|
4 |
24 = un hyper cube |
16 : 16 V , 32 R. |
With greatfull help from Mr Silvain Thisy
Remember:
Topology of surfaces such as defined by Euler (1707-1783, been born 40 years after the death of Fermat)
V-R + F = X
V=Vertex R=Ridge F=face
Square : 4 Vertexs - 4 Ridges + 1 Face =1
L of topologic odd square : 6 Vertexs - 6 Ridges + 1 Face =1
Slicing volumes:
To extrapolate the study on topologicals squares, I wondered it how much had to cut a volume.
-
What look like a volume greater than a cube?
-
How many Vertexs and Ridges ?
-
Link with formulae divisors of Fermat's polynomes (on top = 1 x 2 x 3 ...)?
Have a look on topologics divisors:
Factorizing 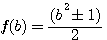 We notice that divisor =
We notice that divisor =
2volume
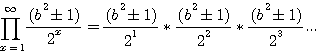
For a cube cube, divide by 4 seams to be closer...
Factorize a cube = 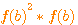 , development ,and study difference
, development ,and study difference
|
|
|
Verification with b=3 for c3
|
|
|
|
|
|
|
|
Verification with b=3 for a3
|
|
|
||
|
|
4374+243+27+1/8 | |
|
|
|
|
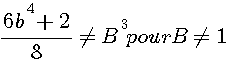 Test with >
Test with >
The equation |
Factorize f(x)^4 ,development, and study difference
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Verifications b=3: 5832+72/16 = 369 = 54 - 44 ,
for b=5 , the topologic SQUARE is 12,13 (13²-12²=5²) : 15650/2 = 7825 = 134 - 124
Premieres conclusions rapide- travail restant à faire
![]() By this guess, I'm not try to prove that
By this guess, I'm not try to prove that 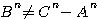 , not possible by Fermat, but to calculate and write the differences of volumes équations (*) CAD:
, not possible by Fermat, but to calculate and write the differences of volumes équations (*) CAD: 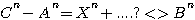 ; To say: Difference between Cn - An , from C²-A², is THIS.
; To say: Difference between Cn - An , from C²-A², is THIS.
Obviously f+(b)f+(b)f+(b)... - f-(b)f-(b)f(b)... because insue of a right-angled primary triangles powered: ^2^3... pacticable ...
![]() Seeing these differences and their exponencial growth greatest than a polygonal number in the power of the same rank, Fermat in been able well to hold this logical reasoning, especially since Diophante evokes a division by 8 in the document annotated by Fermat, and especially since we find the equation x ²-1 / x in the Arithmetica de Fermat (but drowned with others equations evoking the addition of squares and cubes).
Seeing these differences and their exponencial growth greatest than a polygonal number in the power of the same rank, Fermat in been able well to hold this logical reasoning, especially since Diophante evokes a division by 8 in the document annotated by Fermat, and especially since we find the equation x ²-1 / x in the Arithmetica de Fermat (but drowned with others equations evoking the addition of squares and cubes).
Nevertheless I continuous to think that Fermat to analyze rather the differences of its polynomes, especially because he rather drew and study triangles.
![]() The intermediates equations haven't the same interest because it's easier to calculate b4 than
The intermediates equations haven't the same interest because it's easier to calculate b4 than 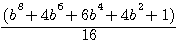 ! , but there are essential for calculate differences.(*)
! , but there are essential for calculate differences.(*)
![]() A lot off people says to me that Fermat haven't a computer but I'm using a computer for present (by this site) datas , animated drawing, matrices... but not for my guess realized manualy (*)
A lot off people says to me that Fermat haven't a computer but I'm using a computer for present (by this site) datas , animated drawing, matrices... but not for my guess realized manualy (*)
(*) But you can use my "µFermaty calculator" for testing and undestand this guess
Don't hesitate to react in Contact me

Patrick Stoltz 05/11/2010 pubished on schemath.com this day – deposit INPI on the way
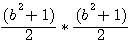
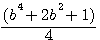
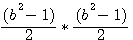
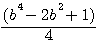
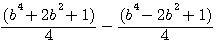 =
= 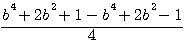 =
= 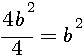
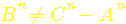
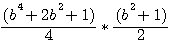
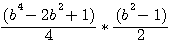
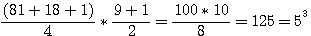
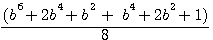
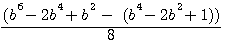
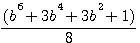
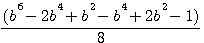
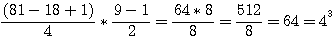
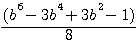
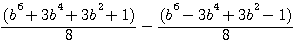
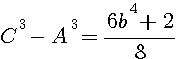
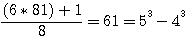
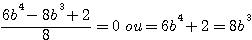
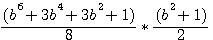
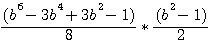
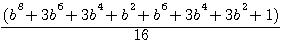
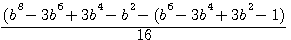
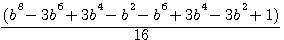
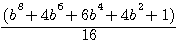
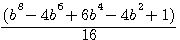
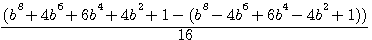
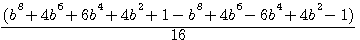
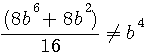 ,
,