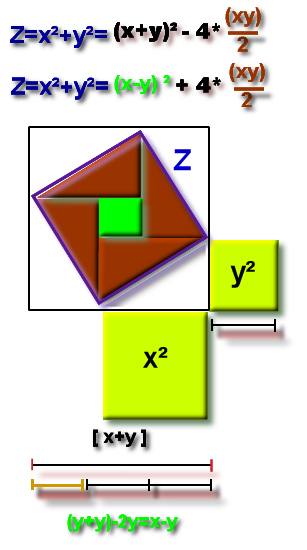
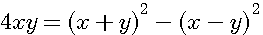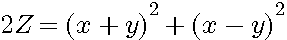Une des notions très importante observée entre autre dans l'arithmetica livre V question 8 est la notion de la double hypoténuse : la surface Z étant x²+y² , 2Z = 2x²+2y²
Démonstration:
Rappel Z=x²+y²
|
(x-y)²=x²-2xy+y² donc |
(x+y)²=x²+2xy+y² donc |
|
x²+y² = 2xy+(x-y)² |
x²+y² = 2xy-(x+y)² |
|
multiplication par 2 de ces équations : |
|
|
2x²+2y² = 4xy+2(x-y)² |
2x²+2y² = 4xy-2(x+y)² |
|
2x²+2y² = 2Z
|
|
|
2Z=(x+y)²-(x-y)²+2(x-y)² -1(x-y)²+2(x-y)²= + (x-y)² |
2Z=(x+y)²-(x-y)²-2(x+y)² 1(x+y)²-2(x+y)²= + (x+y)² |
|
|
|
Exemples : 2²+5² = 29 * 2 = 58 = 49+9 = (5+2)²+(5-2)²
1²+6² = 37*2 = 74 = 49+25 = (6+1)²+(6-1)²
Vérification:
(x+y)²+(x-y)²=x²+2xy+y²+x²-2xy+y²=2x²+2y²=2Z
Parité de 2Z
Cette formule implique que x est pair , y impair ou vice-versa
Si Z = (2x²)+(2y²) alors Z=4x²+4y² => 4Z=4(x²+y²)
surface 1Z=1x²+1y²
2xy = 4* (xy)/2
Notez que 2x² ou 2y² NE SONT PAS DES CARRES
4Z <> 2Z
Ce qui implique que (x+y)² et (x-y)² sont impairs :
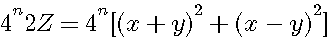
2Z divisible par 4n
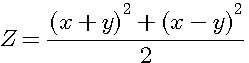
(x+y)²/2 ou (x-y)²/2 est différent de [(x+y)/2]² ou [(x-y)/2]²
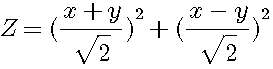
2z=2x²+2y²
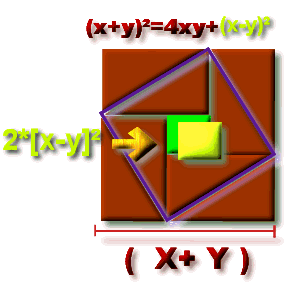
2Z = 8*(xy/2) + 2* (x-y)²
= (x+y)²+(x-y)²
