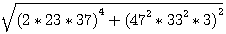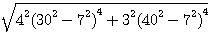Livre V , Question 8 : Trouver trois triangles rectangles de même aire
Trouver 3 triangles rectangle de même aire
Considérons l'expression 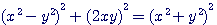 , Diophante cherche deux nombres dont le produit , plus la somme des carrés , fasse un carré. , Diophante cherche deux nombres dont le produit , plus la somme des carrés , fasse un carré.
|
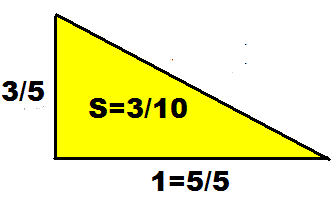
Solution : La question précedente donne pour ces nombres 1 , 3/5 , ou 5 et 3.
Si on multiplie les cotés par 5 : 3/5 * 5 = 3 et 1*5 = 5
(Voir le tableau et explications ci-dessus)
On trouve en effet 5² + 3² + 5 x 3 = 7².
Celà posé , on remplace dans la formule x et y par 3,7 par 5,7 par 7, 3+5 = 8 , et on forme les trois triangles rectangles : 40, 42 , 58 ; 24 ,70,74 : 15,112,113 dont l'aire est 840.
|
 |
|
(40 * 42)/2 = 840 , (24*70) / 2 = 840 , (15*112)/2 = 840
Nota : Je reproduit trés scrupuleusement les équations tels qu'écrites , mais je constate que Y étant plus grand que x , x² - y² est négatif et devient positif avec sa mise au carré .. .
Pas facile à comprendre ,vérifions ces nombres dans un tableau.
|
|
 La surface 840 = 3 x 5 x 7 x 8 La surface 840 = 3 x 5 x 7 x 8
 la surface 2xy(y²-x²)/2 est égale à xy(y²-x²) la surface 2xy(y²-x²)/2 est égale à xy(y²-x²)
| x |
y |
(y²-x²) |
2xy |
(x²+y²) |
2xy*(y²-x²)/2 |
| 3 |
7 |
40=5x8 |
42=2*3*7 |
58 |
840=3x7x5x8 |
| 5 |
7 |
24=8x3 |
70=2*5*7 |
74 |
840=5x7x8x3 |
| 7 |
8 |
15=3x5 |
112=2*7*8 |
113 |
840=7x8x3x5 |
|
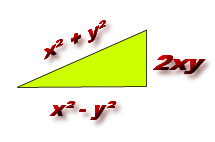
Représentation en un triangle rectangle de la formule (x²-y²)² + (2xy)² = (x²+y²)² : Ses cotés x²-y² et 2xy son Hypothénuse = x²+y² ,
Exemple x=3 y = 7
|
(x²-y²)
|
2xy
|
H=x²+y²
|
|
7²-3²=40
|
2*3*7=42
|
3²+7²=58
|
|
Diophante choisi les nombres de la question précédente car si x² + xy +y² est un carré, x² + 2xy + y² est aussi un carré, en effet : 3² + 3x5 +5² = 7² , 3² + 2 x (3x5) + 5² est aussi un carré c'est à dire 9 + 30 + 25 = 64 = 8²
|
3²
|
+ 3 x 5
|
+5²
|
|
|
|
= 7²
|
+ 3 x 5
|
= 8²
|
Equation Diophantesque : n²+n = n(n+1)
Remarquons toute l'astuce de ces nombres , quand x et y sont deux des quatres nombres du produit 3 x 5 x 7 x 8 , x²-y² sont les deux autres nombres:
Si nous prenons les chifres de Diophante 3² + 3*5 + 5² + 3*5 = 8² et que nous passons un des deux 3*5 dans le terme de droite alors nous obtenons une triple égalité : 3² + 3*5 + 5² = 8² - 3*5 = 7²
|
Triple égalité :
(7²) = (7²) = 7²
|
Dans l'équation (7²=7²):
3²+3x5+5²=8²-3*5
on passe 3² ou 5² à droite
|
Factorisation n²+n = n(n+1) dans le terme de gauche
n=5
n=3
|
Ce qui détermine X et Y pour les 2 premiers cas :
|
|
(3²+3x5+5²) = (8²-3*5) = 7 ²
|
3x5+5²= (8²-3*5)- 3²
|
5(5+3) = 7²-3²=5x8
|
Y=7 et X = 3 |
|
3²+3x5 = (8²-3*5) - 5²
|
3(5+3) = 7²-5²=3x8
|
Y=7 et X = 5 |
Pour le troisiéme triangle de même aire , le procédé est plus simple , nous n'avons besoin que d'une double égalité :
|
7² + 3x5 = 8²
|
8² - 7² = 3 x 5
|
y=8 et x=7 |
Vision graphique des surfaces de carrés de Diophante
|
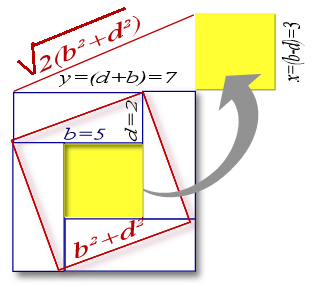
Visualisation graphique du chapitre ci contre:
Rechercher l'équivalence b et d par raport au terme x²-y²
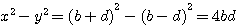
Au lieu de chercher à taton dans un produit ces deux termes (bd) , voyons ci-contre une méthode plus simple l'axiome de Diophante:
Pour d:
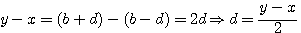
Visuellement : y-x = les 2 largeurs d
Pour b: 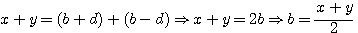
Exemple : Somme de deux nombres = 8 (b+d)
Différence de deux nombres (b-d) = 7
Par la premiére méthode :8²-7²=15 divisé par 4 !!! = 15/4 ... b=15/2 d=1/2
Part la deuxième méthode : d=(8-7)/2 = 1/2 ; b= (8+7)/2 = 15/2
|
Si dans l'expression
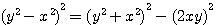
j'introduis, comme le préconise Diophante dans son exemple, les nombres y=7 et x=3 alors je recherche à quelles nombres , b et d, correspond la somme 7 et la différence 3 dans le terme de gauche (y²-x²)²= ... c'est à dire :
(y²-x²)² => ((d+b)²-(d-b)²)²
J'applique donc la formule (b+d)²-(b-d)²=4bd (décrite dans l'"axiome de Diophante au Livre 1 question 30)
pour trouver ces deux nombres décris par Fermat (ci dessous) comme étant un "triangle de base". En fait je remplace X par (d-b) et Y par (d+b)
7² (49 ) - 3² (9) = 4*10 , 10 étant le produit de 5 et 2 alors ce "triangle de base" est composé de b=5 et d=2 : L'hypothénuse carré de ce triangle de base étant 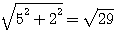
|
 Le terme (y²-x²)² =>((d + b)²-(d - b)²)² équivaut dans l'exemple à : Le terme (y²-x²)² =>((d + b)²-(d - b)²)² équivaut dans l'exemple à :
((5 + 2)² - (5-2)² )² = (7² - 3²)² = 40²
 Le terme (y²+x²) - (2xy)² = dans l'éxemple à : Le terme (y²+x²) - (2xy)² = dans l'éxemple à :
((5 + 2)² + (5 - 2)²) ² - (2 * (5 + 2)(5 - 2))² =
(7² + 3²)² - (2*7*3)² = 58² - 42² = 40²
Ce principe fonctionne aussi pour les nombres de Diophante 7 et 5 et pour 8 et 7.
|
Y
|
X
|
b
|
d
|
|
7
|
3
|
(7-3)/2=2
|
(7+3)/2=5
|
|
7
|
5
|
(7-5)/2=1
|
(7+5)/2=6
|
|
8
|
7
|
(8-7)/2=1/2
|
(8+7)/2=15/2
|
|
|
Remarque importante: La somme de deux nombres au càrré moins la différence de deux nombres au carré égal 4 fois le produit de ces deux nombres :
(b + d)² - (b - d)² = 4bd
La somme de deux nombres au càrré plus la différence de deux nombres au carré égal deus fois la somme du carré de ces deux nombres :
(b + d)² + (b - d)² = 2(b² + d²)
OBS de Fermat. Mais peut-on trouver 4, ou plusieurs triangles rectangles en nombre infini, de même aire. Rien ne paraît s'opposer à ce que la question soit possible, celà sera recherché ulterieurement; nous avons de plus construit ce problème : Etant donné l'aire d'un triangle, trouver une infinité de triangles recatangles de même aire.
Etant donné l'aire , 6 qui appartient au triancle rectangle dont les coté sont 3 , 4 , 5 , en voici un autre de même aire : 7/10 , 120 / 7 , 1201/70, ou si l'on veut le reduite au même dénominateur : 49/70 , 1200/70 et 1201/70.
|
Le triangle rectangle de coté :
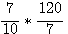
a bien une surface de 6 (rectangle de 120/10 = 12 , divisé par 2 pour la surface du triangle rectangle.)
|
 Un triangle de coté 3 et 4 , à pour surface 12/6 = 6 Un triangle de coté 3 et 4 , à pour surface 12/6 = 6
 Par produit en croix les cotés, Par produit en croix les cotés, 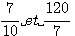 produisent deux nouveaux cotés 7*7 et 120*10 C'est à dire 49 et 1200 (dont l'hypothénuse est 1201) produisent deux nouveaux cotés 7*7 et 120*10 C'est à dire 49 et 1200 (dont l'hypothénuse est 1201)
|
|
Notre méthode constante et perpétuelle est celle-ci ; Qu'on prenne un triangle quelconque dont l'hypothénuse soit z, la base b , la hauteur d , de celui-ci on déduit un autre triangle rectangle dissemblable de même aire ; il est formé de z² et de 2db , en appliquant aux cotés les termes 2zb² - 2zd².
|
|
 Le choix des lettres du "triangle de base" de Fermat est trés habile, en effet un triangle rectangle de base b retourné de 90° devient la hauteur , la lettre d étant le mirroir de b Le choix des lettres du "triangle de base" de Fermat est trés habile, en effet un triangle rectangle de base b retourné de 90° devient la hauteur , la lettre d étant le mirroir de b
J'attribue la note suivante à Emile Brassine , les équations litérales tels qu'on les connaissent n'exixtant pas encore...
La formule générale du triangle rectangle est :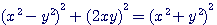 , si on fait dans cette formule x = z² = b²+d² ; y =2bd , on trouve aisément , en divisant par 2z(b²-d²) que les cotés du triangle rectantgle sont : , si on fait dans cette formule x = z² = b²+d² ; y =2bd , on trouve aisément , en divisant par 2z(b²-d²) que les cotés du triangle rectantgle sont :
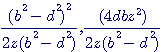 et l'hypothénuse et l'hypothénuse 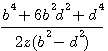
|
Note importante sur z et z²
Soit un triangle rectangle de coté 5 et 12 ,
son hypothénuse z sera = à 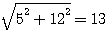 et et
son hypothénuse au CARRE , z² sera = à
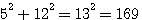
|
Vision numérique :
Appliquons l'exemple de Fermat du triangle 3,4,5 à cette formule pour y voir un peu plus clair... b=4 d=3 z=5 z²=25
|
1er coté:
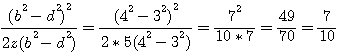
|
2éme coté:
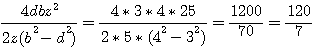
|
|
Hypothénuse:
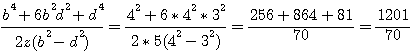
|
 On peut simplifier les deux cotés : On peut simplifier les deux cotés : 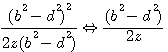 et et 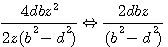
 Dans cette relation ; puisque 49² + 1200² = 1201² alors Dans cette relation ; puisque 49² + 1200² = 1201² alors 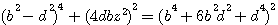
 2z(b²-d²) est un dénominateur commun et ne varie pas 2z(b²-d²) est un dénominateur commun et ne varie pas
Vision arithmétique:
Remplaçons dans 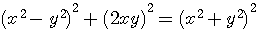 avec les valeurs données par Fermat , x=b²+d²=z² et y=2bd avec les valeurs données par Fermat , x=b²+d²=z² et y=2bd
|
1er coté:
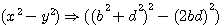
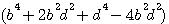
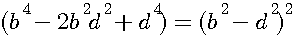
|
2éme coté:
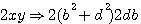
Puisque x²=b²+d²=z² alors
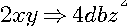
|
|
Hypothénuse:
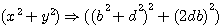
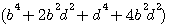
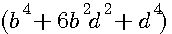
|
Ce nouveau triangle aura une aire égale à l'aire du précédent ; de ce second triangle, par la même méthode un troisième sera formé , du troisième au quatrième, du quatriéme un cinquième, et il sera fait à l'infini des triangles dissemblables de même aire ; et qu'on ne doute pas qu'on en puisse avoir d'autres que les trois donnés par Diophante, savoir : 1° 40,42,58 : 2° 24,70,74 ; et 3° 15,112,113 , ajoutns
un quatrième dissemblable et cependant de même aire :
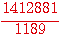 hypothénuse , hypothénuse , 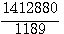 base , base , 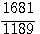 hauteur. hauteur.
A partir de ce point, il m'a été trés difficile de reconstitué ces chiffres , surtout le dénominateur commun 1189 , j'ai donc décomposé ces nombres (issus d'une simplification ?) pour retrouver d et b et pour trouver de quel triangle Fermat nous parle...
Si l'on remplace tel que nous le dit Fermat d=49 , b=1200 , z=1201 à partir de ses nombres de l'exemple 3,4,5 l'on obtient , aprés simplification, deux nouveaux cotés :
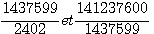 de surface 6 de surface 6
En fait , aprés avoir décomposé 1189 comme étant = à 41 * 29 , (20+21)*29 , et extrapoler b=21 , d=20 (b=42 et d=40) ,j'en conclus que dans ce paragraphe Fermat nous parle des triangles de Diophante ,de surface de 840 (et non pas de surface 6)... Vérifions avec b=42 , d=40 et z=58
|
Hypothénuse:
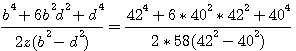
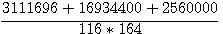
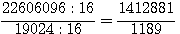
|
base:
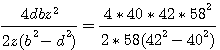
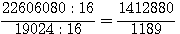
nota (1189 = 41*29)
|
|
hauteur:
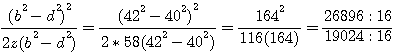
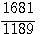
|
La surface du rectangle ainsi obtenu 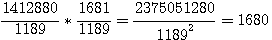 qui divisé par 2 donne bien une surface de 840. Il faut immaginer que Fermat faisait tout ces calculs à la main ... qui divisé par 2 donne bien une surface de 840. Il faut immaginer que Fermat faisait tout ces calculs à la main ...
Ces triangles , par la réduction au même dénominateur , donneront , en nombres entiers, les suivants de même aire
|
Premier
|
47560
|
/1189=40
|
49938
|
/1189=42
|
68962
|
/1189=58
|
|
Second
|
28536
|
/1189=24
|
83230
|
1189=70
|
87986
|
/1189=74
|
|
Troisième
|
17835
|
/1189=15
|
133168
|
1189=112
|
134357
|
/1189=113
|
|
Quatrième
|
1681
|
/ 1189 = 41/29
|
1412880
|
1189=48720/41
|
1412881
|
1412881/1189
|
De la même manière on trouvera à l'infini des triangles rectangles de meme aire ; et la question suivante sera un pas au delà des limites posées par Diophante :
Voici par une autre mèthode, un triangle dont l'aire est égale à six fois un carré , comme pour le triangle 3 , 4, 5 ; savoir 2896804 , 7216803 , 7776485.
La signification de 6 fois un carré est pour le moins mystèrieuse...
Dans un premier temps , décomposons 2896804 , 7216803, 7776485 pour trouver la méthode de Fermat !!! et dire que de tels carrés furent trouvés sans calculatrice !!!
|
2896804
|
7216803
|
|
= 1702² = (2x23x37)²=4x23²x37²
|
47²x11²x3²x3 = 47²x33²x3
|
|
Hypothénuse = 7776485
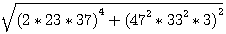
|
Moi , par contre , heureusement j'en avais une....
Méthode de recherche selon question 7:
Aprés quelques recherches , j'ai appliqué ces chiffres au tableau formé par l'équation de Diophante de la question 7 , n²+n+1 = (n-2)² , (et nojn pas question 8) pour proposer ce tableau :
| 23² |
+840 |
|
|
33² |
+280 |
|
| = 37² |
+840 |
|
= 37² |
+840 |
| =47² |
Ce qui ne m'a pas inspiré grand chose , sauf que Fermat nous parles de diférents carrés de 840 ...
Méthode de recherche selon question 8:
Si j'applique la rechercher l'équivalence b et d par raport au terme x² et y² .sur ce triangle nous obtenons les résultats suivants:
Dans le premier terme de ce triangle rectangle 2896804 = 4x37²x23² Si je considére 37 comme une somme et 23 comme une différence, et que je recherche les 2 nombres d+b = 37 et d-b = 23 :
d= (37+23) / 2 = 30 et b = (37-23) / 2 = 7 , ce qui me donne : 2896804 = 4 * 37² * 23² = 4(30 + 7)²(30² - 7²)² = 4(30²-7²)²
Pour le deuxième terme : 7216803=3 * 47² * 33² = 3(40+7)²(40-7)²=3(40²-7²)²
|
2896804
|
7216803
|
|
4 (30² - 7²)²
4*(851)²=2896804
|
3 (40²-7²) ²
3*(1551)²=7216803
|
|
Hypothénuse = 7776485
|
|
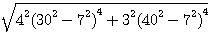
|

|

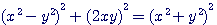 , Diophante cherche deux nombres dont le produit , plus la somme des carrés , fasse un carré.
, Diophante cherche deux nombres dont le produit , plus la somme des carrés , fasse un carré.


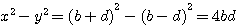
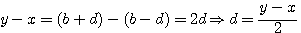
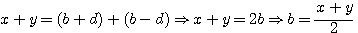
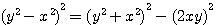
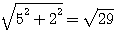
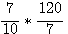
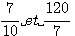 produisent deux nouveaux cotés 7*7 et 120*10 C'est à dire 49 et 1200 (dont l'hypothénuse est 1201)
produisent deux nouveaux cotés 7*7 et 120*10 C'est à dire 49 et 1200 (dont l'hypothénuse est 1201)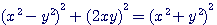 , si on fait dans cette formule x = z² = b²+d² ; y =2bd , on trouve aisément , en divisant par 2z(b²-d²) que les cotés du triangle rectantgle sont :
, si on fait dans cette formule x = z² = b²+d² ; y =2bd , on trouve aisément , en divisant par 2z(b²-d²) que les cotés du triangle rectantgle sont :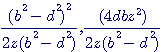 et l'hypothénuse
et l'hypothénuse 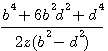
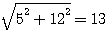 et
et 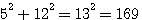
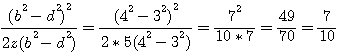
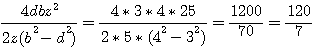
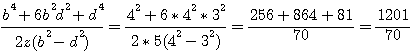
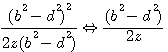 et
et 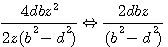
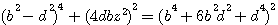
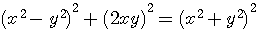 avec les valeurs données par Fermat , x=b²+d²=z² et y=2bd
avec les valeurs données par Fermat , x=b²+d²=z² et y=2bd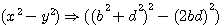
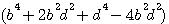
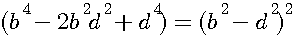
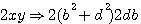
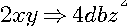
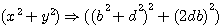
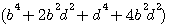
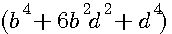
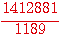 hypothénuse ,
hypothénuse , 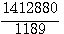 base ,
base , 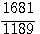 hauteur.
hauteur.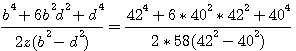
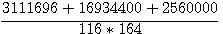
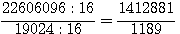
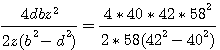
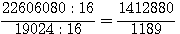
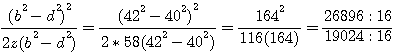
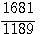
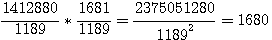 qui divisé par 2 donne bien une surface de 840. Il faut immaginer que Fermat faisait tout ces calculs à la main ...
qui divisé par 2 donne bien une surface de 840. Il faut immaginer que Fermat faisait tout ces calculs à la main ...