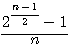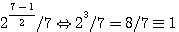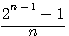Dans la suite de cette étude , je cherche à visualiser les nombres premiers, leurs répartitions et les moyens de reduire les grandes puissances de 2...
Pour ce faire, j'utilise la topologie des carrés ainsi formés (selon le meme principe) pour affiner/infirmer cette conjecture.
Topologie de 2n pair et impair
La topologie des carrés formés par 2n est different selon n pair et impaire
Pour obtenir une racine entière d'un carré pair (en binaire par exemple) il suffit de diviser l'exposant par 2
Exemple: 28 = à un carré de 24 * 24 , 256 est un carré de 16*16
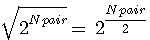
Par contre pour obtenir un carré de 2 impair il faut:
Diviser ce nombre par 2 (ou appliquer 2 n-1), puis former un rectangle composé de 2 carrés pair dont le petit coté est = à la racine du carré pair et le grand coté 2 * la racine du coté pair
Exemple: 25 = à un rectangle de 2 (5-1)/2 * 2(2 (5-1)/2) ou (2 (5+1)/2)
25 = 22 * 23 , 32 est un rectangle de 4 * 8
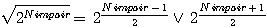 (V signifie OU)
(V signifie OU)
V = ou sera expliqué dans les paragraphes suivants
'illustration graphique du dépliage des 2n /visualisation de la composition d'un nombre premier multiple de 4 selon Fermat
Topologie de la conjecture 2 n-1 -1 / n mod 1 =0 est premier
|
|
Par definition un nombre premier est impair (sauf 2) , ils sont dans un ensemble de nombres bien précis. Comme le démontre Riemann, les nombres premiers impairs sont rangés dans l'axe 1/2 + it , les nombres pairs étant négatifs si n premier est toujours impair, n-1 est donc un exposant toujours pair. Donc selon
Cette conjecture démontre graphiquement la Théorie des deux carrés de Fermat (tout nombre premier divisé par 4 est congrus à 1)
ci contre : Ce carré de 24 a un coté de 22 |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||




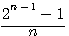 ,tout nombre premier est inscrit dans une topologie d'un 2
,tout nombre premier est inscrit dans une topologie d'un 2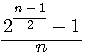
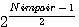
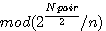

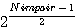 = r
= r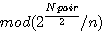 = reste de la division du coté du carré par n
= reste de la division du coté du carré par n