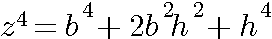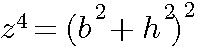La descente infinie selon Pierre de Fermat

Livre VI Question 20

Trouver un triangle rectangle tel , que l'aire, ajoutée à l'hypoténuse fasse un cube et que le périmètre soit un carré.

La solution à ce problème ,à mon sens, n'est pas fondamentale , L'observation de Fermat l'est plus.

OBS.DE FERMAT : L'AIRE d'un triangle RECTANGLE exprimée en nombre entier ne peut être égale à UN CARRE.

Introduction , Rappels

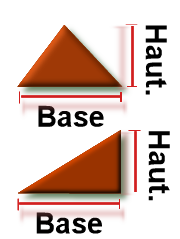
Rappel sur l'aire d'un triangle RECTANGLE:

L'aire d'un triangle QUELCONQUE étant égale à Base*Hauteur /2 , que le triangle soit quelconque ou rectangle , son aire sera la même (schema N°1).

Ainsi l'aire d'un triangle quelconque exprimée en nombre entier peut être égale à un carré.

Par exemple si la base = 18 et hauteur = 4 alors son aire sera 18*4=72 /2 = 36 = 6²

Il faut donc différencier la nature d'un triangle QUELCONQUE et un triangle RECTANGLE.

Schema N°1

Surface = B*H/2

Différence entre un triangle rectangle et quelconque.

Soit le triangle rouge du schema n°2, sa surface exprimée en nombre entier sera Base*Hauteur/2 .

Mais, parce que ce triangle est RECTANGLE, il existe aussi une surface Z= z'² = Base² + Hauteur² telle que z'²-Base²=Hauteur² ou z'²-Hauteur²=Base².

Tel que représenté sur le schema n°2, si Z est un carré alors les cotés des 3 carrés z',Base,Hauteur sont des nombres ENTIERS (ou sont fractionnaires entier).

Et surtout : z'² - Ht² = [z'+Ht]*[z'-Ht] =UN produit d'au moins deux nombres entiers égal à UN CARRE  (ou z'² - Base² =[z'+Base]*[z'-Base] )

Par exemple 65²=39² + 52² nous donne :

65²-39² = (65+39)(65-39)= 104*26 =4²13²=52²

Notez que 104 à lui seul n'est pas un carré : 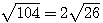  et 26 non plus :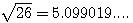 

65²-52²=(65+52)(65-52)=117*13 = 3²*13*13=3²13²=39²

117 n'est pas un carré et 13 non plus

Détails :

Schema N°2

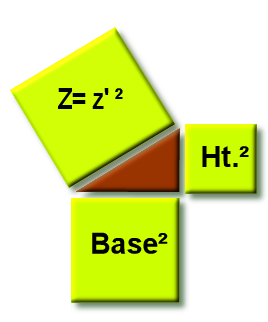
Le coté de Z = z'

Le coté de Ht² = Ht

Le coté de Base² = Base

Surface =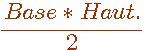

Selon Fermat

Surface² =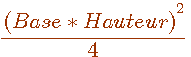

est impossible

Rappel sur l'équation de Diophante

Soit l'équation de Diophante :

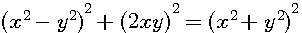
On note que la surface (x²-y²)² = [(x+y)(x-y)][(x+y)(x-y)] =

(x+y)²(x-y)²

Page détaillée

Le théorème de Fermat du Livre 6 Question 20

OBS.DE FERMAT : L'aire d'un triangle rectangle exprimée en nombre entier ne peut être égale à un carré.

Nous placerons ici la démonstration de ce théorème, de notre invention , que nous avons découvert apés une laborieuse et pénible méditation. Ce genre de démonstration produira de merveilleux progrès dans les questions arithmétiques.

Si l'aire d'un triangle ETAIT un carré , on donnerait deux quatrièmes puissances dont la différence serait un carré.

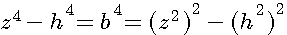
ou

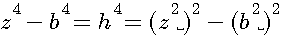
Ce qui donnerait les cotés du triangle rouge = b² , h² ,z²

D'ou il suit qu'il SERAIT donné deux carrés dont la somme et la différence SERAIENT des carrés.

Soit l'identité remarquable a²-b² = (a+b)(a-b) si a=z² et b=h² alors (selon schema N°3 h<b)

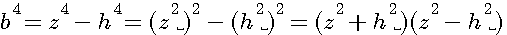
Donc on devrait s'attendre à ce que le produit (z²+h²)(z²-h²) soit un carré égal à (b²)²

Schema N°3

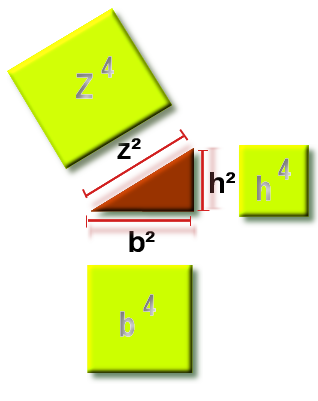
h=hauteur , b= base du triangle rectangle rouge

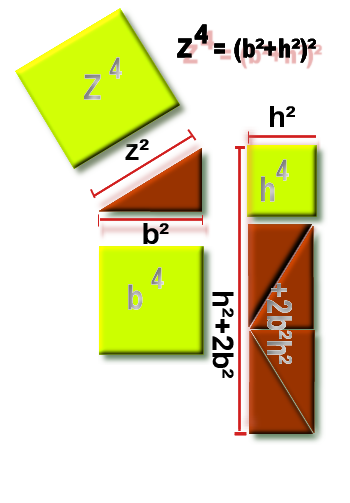
Z⁴-h⁴ est t'il égal à b⁴ ? Ce qui donnerait ce coté = b²

de même que :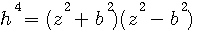

Le premier facteur de b⁴=(z²+h²)(z²-h²) , (z²+h²) est aussi égal à (z²-h²+2h²) donc:

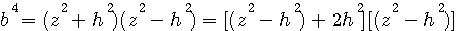
Distribution du 2ème facteur (z²-²²) dans le premier

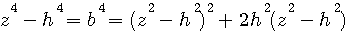
puisque que nous sommes certain que (selon pythagore) z²=b²+h² alors z²-h²=b² (z,h,b ou fractionnaire)

Dans (z²-h²)²+2h²(z²-h²), remplaçons (z²-h²) par b²

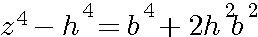
Voir : schéma N°4

ou si Z⁴-b⁴

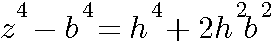
Voir : schéma N°5

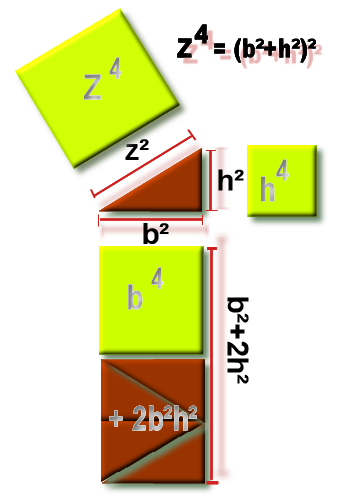
Comment cela est t'il possible  ? z⁴-h⁴ = b⁴ + quelque chose? (selon schéma N°4)  

Tout simplement parce que z⁴ et b⁴ sont deux volumes (appelés Hypercubes) de HAUTEURS DIFFERENTES.

Ainsi est donné un nombre formé d'un carré et du double d'un carré qui est égal à un carré, avec cette condition que les carrés qui le composent fassent aussi en somme un carré 

La surface z⁴-h⁴ est un rectangle composée d'un carré (b²)² et du double d'un autre carré 2h²b²=2(hb)² avec cette condition que b²+h²=z².Voir : schéma N°4

ou

La surface z⁴-b⁴ est un rectangle composée d'un carré (h²)² et du double d'un autre carré 2h²b²=2(hb)² avec cette condition que b²+h²=z².Voir : schéma N°5

Nous en déduisons aussi  :

identité remarquable a²-b² :

a²-b² = (a+b)(a-b)

si a= (a²) b=(b²) =>

(a²)^²-(b²)^²=[(a²) + (b²)][(a²) - (b²)]

Raccourci si b²+h²=z² alors:

(z²)²-(h²)² = (b²+h²)²-(h²)²

a=(b²+h²) b=h² donc (a+b)(a-b)=

(b²+h²+h²)(b²+h²-h²) =>

(z²)²-(h²)² = (b²+2h²)(b²) =

Schema N°4 : Z⁴-h⁴

MAIS SI un nombre carré est la somme d'un carré et du double d'un autre carré, son coté est pareillement la somme d'un carré et du double d'un carré , comme nous pouvons facilement le démontrer.

D'où il SERAIT conclu que ce coté est la somme des cotés de l'angle droit d'un triangle , et qu'un des carrés est la base et que le double carré est égal à la hauteur

Revenons donc à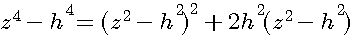

ou

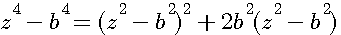
Nous sommes certains que si z² = b²+h² est un carré alors z²-h²=b² et z²-n²=h²

Ce qui nous donne dans les deux cas 2b²h² (=2h²b²) et donc pour le premier terme (un des carrés qui est donc selon Fermat la base de ce nouveau triangle):

(z²-2h²)²  ou (z²-2b²)²

Puisque z²=b²+h² donc le premier terme =

(b²+h²-2h²) = (b²-h²)² ou (b²+h²-2b²) = (h²-b²)²

Schema N°5 : Z⁴-b⁴

Ainsi ce triangle rectangle sera formé de deux carrés dont la somme et la difference seront des carrés.

Somme des 2 carrés:

Mais on prouvera que ces deux carrés sont plus petits que les deux premiers carrés supposés, dont la somme aussi bien que la différence font un carré.

Donc , si on donne deux carrés, dont la somme et la différence font un carré , on pourra donner en nombres entiers la somme de deux carrés de même nature qui sera moindre que la première .

Par le même raisonnement on en trouvera un moindre que celle qui a été trouvée par le procédé qui a fait trouver la première , et toujours jusqu'a l'infini , on trouvera des nombres entiers moindres ayant la même propriété , ce qui est impossible , parce qu'on ne pas donner un nombre infini de nombres entiers moindres qu'un nombre entier quelconque.

L'exiguïté de la marge nous empêche d'insérer la démonstration complète , et plus amplement expliquée.

Par ce procédé nous avons conçu et confirmé par démonstration qu'aucun nombre triangulaire , à l'exception de l'unité , ne pouvait être égalé à une quatrième puissance.