Preface

Contexte historique :

L'arithmetica de Diophante (environ 200-300) est une liste de questions arithmétiques contenues dans VI livres . Par la suite,l' arithmetica fut étudié et annoté par Bachet (1581-1638), par Fermat (1601-1665) et en 1853 par Emile Brassine (*), professeur à l'école impériale d'artillerie de Toulouse.

 

Diophante ne connaissait pas le zéro, Fermat n'utilisait pas le zéro géométrique, il ne dessinait pas les axes des abscisses et ordonnées (cf: Opéra varia de Fermat) . Ils ne connaissaient pas les nombres négatifs en tant que tel et bien sûr les nombres réels.

A l'époque de Pierre de Fermat, la notation algébrique (Utilisation des lettres dans une équation) en est à ses débuts. Il me faut vous citer un autre mathématicien amateur : François Viette (1540-1603) dont les travaux ont grandement fait avancer les équations telles que nous les connaissons aujourd'hui .

Exemple : si Diophante dit : si le double produit l'un nombre égale 10 alors ce nombre = 5 , se note aujourd'hui 2x = 10 => x=5

 

C'est au cours de l'étude du livre II paragraphe 9 de l'Arithmetica de Diophante que Fermat a posé son grand théorème et il est dit que Fermat ne disposait pas d'outils mathématiques suffisants pour énoncer son Grand théorème puisqu'il a été démontré par Andrew Wiles environ 300 ans plus tard (10 ans d'études, 200 pages, seuls quelques mathématiciens pouvaient la comprendre) ..

 

Mes recherches :

 

J'ai entrepris depuis de nombreuses années d'étudier de détailler et de reconstituer si possible les équations (et matrices) correspondantes aux notes et nombres de Pierre de Fermat qu'il a faits sur l'Aritmetica de Diophante:

  • En m'aidant des notes d' Emile Brassine (*) , Diophante et Bachet

  • En reconstituant les équations littérales en équations algébriques à partir des seuls nombres cités par Fermat : Exemple sur la question 2 du Livre IV l'équation

  • En visualisant ces théories dans des diverses matrices (tableaux) et schemas.

  • En regardant quels algorithmes et théorèmes Fermat cite t'il le plus fréquemment ? son Petit Théorème ?

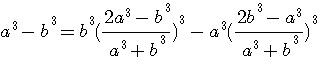
Au cours de cette étude (à ce jour) il s'avère que ses annotations les plus récurentes ne sont pas, comme on pourrait s'y attendre, une certaine descente infinie , son petit Théorème, ou des triangles de Pascal...  mais sont quasiment toutes relatives à des SURFACES.

fleche_animée Les nombres polygonaux et triangulaires sont des répresentations en surfaces des nombres (par exemple un carré est décomposé en 2 nombres triangulaires consecutifs)

fleche_animée Les hypothénuses sont étudiées par leurs surfaces : (x²+y²)²

L'hypoténuse première d'un triangle rectangle de forme x²+y² = 4n+1 (théorème des deux carrés) cité entre autre dans le Livre III question 22  , Livre V question 12 , Livre V question 24

Dans cette étude je détaille entre autre :

L'existence d'un "triangle de base" de cotés d et b cité par Pierre de Fermat dans Le Livre V question 7 et 8 et son Opera Varia

fleche_animée Nombre d'or et équation du second degrés Livre I question 30

fleche_animée La partie restante non détériorée du Livre "Des Nombres Polygonaux"

fleche_animée La descente infinie selon Fermat Livre VI question 20

 

(*) Oeuvres mathématiques et de l'arithmétique de diophante par Emile.Brassine aux éditions Jacques Gabay