|
|
 |
||||||||||||
Dans ce Livre sur les nombres polygonaux de Diophante dont il ne reste que quelques fragments Diophante aborde : Dans les Questions N°1,N°2 et N°3: Les progressions arithmétiques Dans la Question N°4 Diophante raproche les progressions arithmétiques et les nombres polygonaux Dans la question N°5 , N°6 et N°7 les nombres polygonaux et les équations du second degrés |
|||||||||||||
Les progressions arithmétiqueDéfinition Une progression arithmétique est une suite de nombres dont la différence d'un nombre de cette suite et du nombre précédent est constante. Cette différence est appelée: Raison Exemple : 10,20,30,40 , 40-30 = 10 , 30-20 = 10 .... la raison =10 Cette séquence 10,20,30,40 comporte 4 éléments , le premier élément = 1*raison , le deuxiéme = 2*raison ..... n*raison est la valeur du nième élément Dans mon exemple le 7éme élément de ma progression arithmétique vaudra 70 C.A.D 7*raison La somme de cette séquence sera = raison(1+2+3+4) ... , comme la raison est un facteur commun à tous les éléments de cette séquence alors la raison sera appelée k:
Nous verrons par la suite que dans une équation du second degrés an²+bn+c=0 k=a... Debut de séquence = 0 Soit la séquence exemple 10,20,30,40 , le premier élément = 10 (=1*k) est bien = à la raison - l'élément précèdent qui est zéro !!! Donc il faut bien considérer le début de cette séquence comme étant égale à zéro C.A.D 0,10,20,30,40 comportant maintenant 5 éléments , chaque élément de cette séquence étant égale à (n-1)K , par exemple le 3ême élément: 20 = (3-1)*10 Début de séquence = a Ce suget est abordé par Diophante dans la question I et II de son livre sur les nombres polygonaux Question II livre des polygonaux : Si cinq nombres a,a+k...a+4k sont en progression arithmétique, l'excès du plus grand sur le plus petit , ou 4k, est un multiple de k exprimé par le nombre de termes moins 1 Diophante nous dit : le 5 éme élément = a+(5-1)K par exemple: a=3 , k=7 => 3,10,17,24,31 le 4éme = 3+ (4-1)*7=24
Début de séquence = a = 1 Dans la suite des questions posées par Diophante dans la question III,IV...Diophante s'intéresse plus particulièrement aux progressions arithmétiques commençant par 1 Question III , livre des polygonaux : Dans une progression arithmétique commençant par 1 et d'un nombre de termes quelconques , la somme de tous les termes par 8 fois la raison , plus le carré de la raison diminué de 2 est un carré. Soit 1,k... 1+(n-1)k, la somme sera Là vous allez me dire que c'est franchement imbuvable, je vais vous démontrer par la suite, pas à pas, que non !!!
Somme d'une progression arithmétique commençant par 1 Reprenons les propos de E.brassine : soit 1,k.... 1+(n-1)k en fait E.Brassine aurait dû écrire 1,1+k ...1+(n-1)k et si la progression commence par 1, chaque terme = 1 + (n-1)K , pour être plus précis nous pouvons écrire 1+ 0K , 1+1k ... 1+(n-1)k
Question VI , livre des polygonaux : Etant donné un nombre N, trouver de combien de manières il peut être polygonal. En appellant P-2 = A , Le texte de Diophante parait altéré , Bachet fait remarquer tout ce qui laisse à désirer. Quoi qu'il en soit , l'on peut supposer que si Diophante pose ce problème alors il maitrisait la résolution d'une équation du second degrés... |
|||||||||||||
|
sous rubriques de l'arithmética
|
|||||||||||||
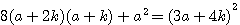
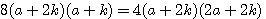
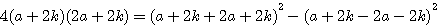
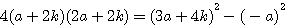
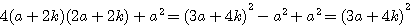
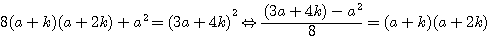
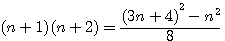
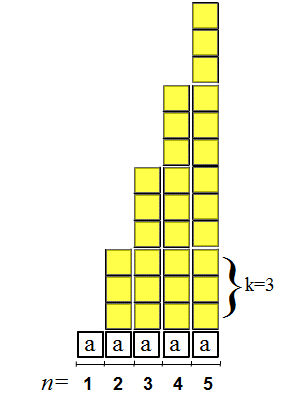
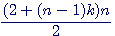 et
et 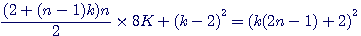
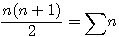
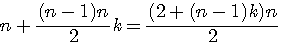
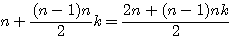 , factorisation par n du numérateur =>
, factorisation par n du numérateur => 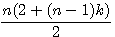
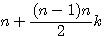 , la somme des nombres d'une progression arithmétique commençant par 1 , si l'on remplace k par (P-2) nous obtenons la
, la somme des nombres d'une progression arithmétique commençant par 1 , si l'on remplace k par (P-2) nous obtenons la 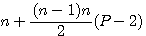 ou P est le nombre de cotés du polygone. Si k= P-2 alors P=k+2.
ou P est le nombre de cotés du polygone. Si k= P-2 alors P=k+2.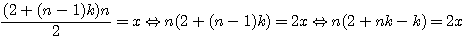
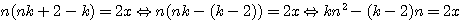
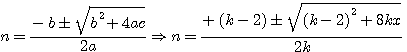
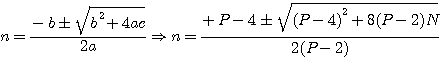
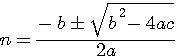
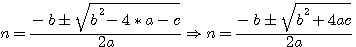
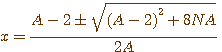 , Si on donnait N, il faudrait trouver le nombre entier A qui rendrait x positif.
, Si on donnait N, il faudrait trouver le nombre entier A qui rendrait x positif. 



