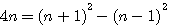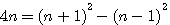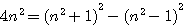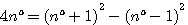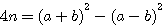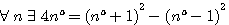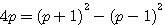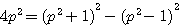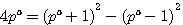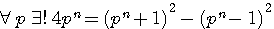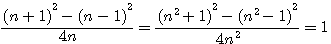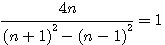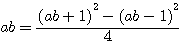|
|
 |
Contacts: Tweet to @schemath |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Cette question n'a pas été annotée par Pierre de Fermat, mais l'équation abordée,
Livre I Question XXX On donne la somme et le produit de deux nombres : trouver ces deux nombres
On donne la somme et le produit de deux nombres : trouver ces deux nombres. Solution. Soit p la somme des deux nombres, q leur produit. Diophante prend pour inconnue x, différence de deux nombres, et il remarque que le produit donné
Cette équation est aussi égale à :
L'on peut démontrer cet équation deux deux manières différentes en utilisant les deux identités remarquables:
Réduction de cette équation du second degrés au premier degrés
Amusons nous avec le problème de Diophante ... Quel sont les deux nombres dont la somme est 13 et le produit et 30 ? (Rappel x est égal à la différence des deux nombres)
Oui mais à ce point nous ne sommes pas forcement plus avancé, celà nous ramenne à connaitre la somme des deux nombres (13 dans l'exemple) et la difference des deux nombres c'est à dire 7 ..... Ce qui nous ammene à poser à quoi est égal
Donc, si (13) - (7) = 6 , alors 2b = 6, b=3 et il nous est maintenant facile de déduire a = 10..(13-3=10)
"L'axiome de Diophante" :
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Si nous divisons les deux termes de l'équation , la relation reste vrai ,égale à 2.
Si nous divisons b par b , la relation reste encore vrai (ce qui est déjà plus curieux) encore égale à 2.
Si nous divisons
Il serait plus juste mathématiquement de remplacer |
Exemple si je prend une simple fraction : Si par contre , je divise une seule des deux fractions le résultat ne sera pas le même : Si je prend maintenant "l'axiome de Diophante" avec 12 et 3 : Je divise donc par 3 les deux termes : Si par contre je divise seulement 12 : Et si je divise seulement 3 :
|
|
|
Le 0 devient un nombre:
Dans la vidéo ci contre outre l'écart de 2 à chaque marche, si je me situe entre la marche -1 et +1 alors la marche 0 à une réalité physique differente de rien.
Si nous supprimont la marche numéro 0 ,si je me trouve au rez de chaussée alors je me trouverai sur la marche -1!!!!
Dans un ascensseur le bouton 0 existe , c'est le rez de chaussée.
Donc cet écart de 2 existe même entre le rez de chaussé (0) , la première marche (+1) et la première marche de la cave (-1)
En binaire,le 0 à aussi un état physique: C'est le complèment à un.
Vidéo (YouTubes) introduction à l'axiome de Diophante |
||
|
Si le zéro à l'espace d'une unité alors le mécanisme de numérotation n'est plus le même:
Complément d'information sur la page l'arithmétique modulaire
Vidéo youtubes suite |
Axiome de Diophante et nombre d'or
|
Dans son "éléments de géométrie" , Euclide à défini le nombre d'or comme étant le rapport (la raison) de , Faisons exactement la même chose avec "l'axiome de Diophante"
Je trouve remarquable de trouver directement, par "l'axiome de Diophante" une valeur à x sans résolution du second degrés.. Remplaçons x par sa valeur Ces deux nombres sont bien égaux (=1.6180....) Appliquons le produit en croix pour vérifier:
L'inverse du nombre d'or
Si x= y alors x/y = 1 ou y/x =1 donc: si
Cet équation resemble beaucoup à la version simplifiée de l'équation de la résolution d'une équation du second degrés.... |
(1) Source : Le nombre d'or par Fernando Combalan Collection le monde est mathématique
Opposé du nombre d'or si x=y alors x-y=0 si Mais aussi (Fermat utilise cet artifice dans le livre iV question 1et2)
|
Cette section est à approfondir, vous pouvez me laisser vos commentaires sur pstoltz@schemath.com
Démonstration du nombre d'or
Inverse du nombre d'or par Fermat
Si la solution du nombre d'or n(n-1) = 1 est 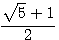 parce que nous avons utilisé la relation 4(2n)(2n-1)+1 = (4n-1)² , Fermat nous donne une autre solution pour un carré impair :4(2n)(2n+1)+1 = (4n+1)² .Nous pouvons donc aussi chercher n(n+1)=1
parce que nous avons utilisé la relation 4(2n)(2n-1)+1 = (4n-1)² , Fermat nous donne une autre solution pour un carré impair :4(2n)(2n+1)+1 = (4n+1)² .Nous pouvons donc aussi chercher n(n+1)=1
|
Soit x(x+1)=1 remplaçons x par 2n
4(2n)(2n+1)+1 = (4n+1)²
|
Vérification , (x)(x+1)=1 , x = 2n =
(a+b)(a-b)=a²-b²
|
Cette 2em valeur est l'inverse de la première 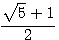 x
x 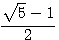 =1
=1
Plus de détails sur Fermat_clef n°3
L'équation fondamentale 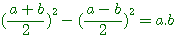
|
Nous allons observer dans ce chapitre si les mécanismes de divisions s'appliquent aussi dans cette équation
.
Division de (a+b)²-(a-b)²=4ab par b ou a
Si l'on divise par b, et non pas par b² l'on obtient une conjecture trés surprenante ce qui reste néanmoins logique puisque le premier terme égale le second, mais néanmoins surprenant car la division porte sur le +b et -b au lieu de (a+b) et (a-b)
Ci dessous, dans quelques tableaux, le mécanisme de cette équation (Formules données pour Open Office): |
|
La première colonne ,b=1, correspond donc à Remarquez que si a=b alors le deuxiéme terme disparait ,(2a)² , ou (2b)² - 0² est bien égal à 2² a x a ou 2² b x b. Mais il existe aussi une deuxième solution :
|
L'on remarque que dans la collone en bleu ,si a=(b+1) alors
Exemple dans la colonne b=3, a=(3+1)=4 : 7²-1=48 divisé par 3 = 16 bien égal 4*4 ou 12+4 En divisant (a+b)²-(a-b)² par b , ou chaque terme par b , l'on obtient 4a, qui est égal à (a+1)²-(a-1)².
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Si ab est un nombre premier (p) alors ce produit devient un nombre premier fois 1 (4ab => 4px1) et il n'existe qu'une seule solution |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Division par a ... = 4b. Mais si , par exemple la somme de deux nombres au carré , moins la difference de deux nombres au carré est égale à un multiple de 4, est ce (1+b)²-(1-b)² qui a été appliqué ou (a+1)²-(a-1)² ? L'on note que pour des puissances pair il n'y a pas de changement mais quel est l'impact pour des puissances impaires? |
Puisque dans cette formule, nous n'intégrons pas b dans la fraction TOTALE au carré, c'est a dire , (a+b)² / b - (a-b)² au lieu de ( (a+b) / b)² - ... alors c'est que nous pouvons inclure au dénominateur dans la fraction TOTALE sa racine carré.
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
L'équation fondamentale 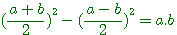 ,les nombres premiers et carrés topologiques impairs (*)
,les nombres premiers et carrés topologiques impairs (*)
Dans dans le Livre III, Question XXII (ainsi que dans son petit théorème) , Fermat introduit (pour la première fois dans l'arithmetica ?) la notion de nombres premiers et de différentes possibilités d'hypothénuse, ce qui a orienter mes recherches pour poser ce premier thérème évident:
Si a (ou b) est un nombre premier (p) alors 4ab devient 4p => 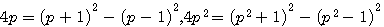 et n'admet qu'une solution
et n'admet qu'une solution
Notez que dans la première expression 4p n'etant pas un carré 4p, p+1,p-1 n'est pas un triangle rectangle entier.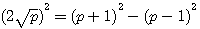
Division par 4
Dans ces deux équations, nous remarquons que le 4 ne change pas , 4p = (p+1)² -... et 4p² = (p²+1)²-... donc dans les deux cas :
.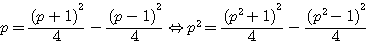
Création d'un nouveau carré
|
4p² étant un carré de coté 2p . Un des cotés d'un triangle rectangle à pour hypothénuse L'autre coté de ce carré Si nous faisons la racine carré entre 4p² et l'hypothénuse
|
Notons que 2p+(p²+1) = (p²+1)² |
Rapport de 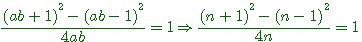 , élévations à toutes puissances,nb possibilités
, élévations à toutes puissances,nb possibilités
En préambule à la Question XXII du LIivre III (Trouver 4 nombres tels que le carré de leur somme, augmenté ou diminué de chacun donne un carré) nous examinons le comportement à toutes puissances du facteur de 4, du nombre de possibilités d'hypothénuses, et de l'impact d'un nombre premier dans un triangle rectangle.
|
Par extention du théorème précedent , si nous remplaçons p par ab (et divisé par 4) nous obtenons le même résultat mais avec au moins deux solutions.
si N à toutes puissances
Notez que cette égalite ne représente pas un triangle rectangle entier , 4n n'étant pas un carré sauf si n=4 (ou une puissance de 4).avec une seule solution D'autre part si n=1 , 4 est aussi un carré mais le deuxieme terme (n-1)² est égal à 0. Si l'égalité demeure vraie 0 ne peux pas ètre un coté d'un triangle. (4 = 2² -0²)
mais aussi si n=a*b
Si n n'est pas premier alors il existe au moins un autre solution.
Pour tout nombre n il existe au moins un ..... N est premier
Si n est premier alors il n'exite qu'une seule solution
Notez également que cette égalité ne représente pas un triangle rectangle
...
Pour tout nombre premier p il existe un seul et unique .... Rapport (raison) de l'expression
Comme dédini par Fermat dans le premier chapitre de son Opera varia
mais aussi
|
Matrice de 4n2, 4n3 et 4n4 et leurs équivalences |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Equation du second degrés par Diophante
(1) Si j'interprète bien la note de Brassine l'équation équivalente serait 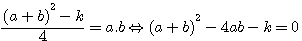 ... a étudier ...
... a étudier ...

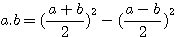 , étant trés similaire à l'équation
, étant trés similaire à l'équation 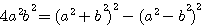 du
du 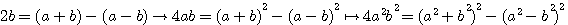
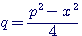 , d'où il déduit x. En général, Diopante ramène l'équation du second degré à la forme x²=k (1) : et pour cet effet , il fait constamment usage de cette relation algébrique qu'il énonce sur des nombres particuliers :
, d'où il déduit x. En général, Diopante ramène l'équation du second degré à la forme x²=k (1) : et pour cet effet , il fait constamment usage de cette relation algébrique qu'il énonce sur des nombres particuliers : 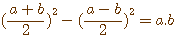
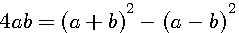 que l'on peut énoncer ainsi
que l'on peut énoncer ainsi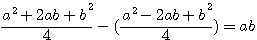
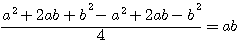
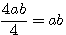
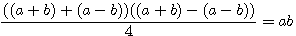
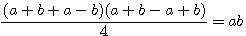
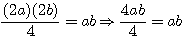
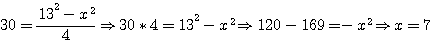
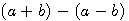 ? C'est à dire (a+b)=13 - (a-b)= 7 ? Vous allez me répondre 6 ... Mais que représente 6?
? C'est à dire (a+b)=13 - (a-b)= 7 ? Vous allez me répondre 6 ... Mais que représente 6?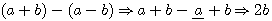
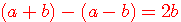
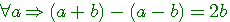
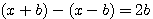 , x peut être n'importe quoi ... ce qui permet en fait d'écrire :
, x peut être n'importe quoi ... ce qui permet en fait d'écrire :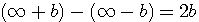
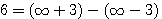 ou
ou 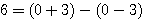 ou
ou 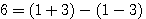 , 6 est considéré comme l'écart entre 3 et -3.
, 6 est considéré comme l'écart entre 3 et -3.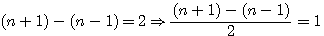 si nous multiplions les deux égalités par
si nous multiplions les deux égalités par 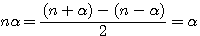 .
.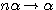 et
et 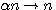
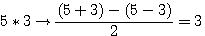 ,
, 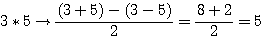
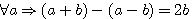 : a = a et peut ètre n'importe quel nombre et peut donc ètre remplacé par mod p
: a = a et peut ètre n'importe quel nombre et peut donc ètre remplacé par mod p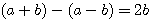 par b.... il se produit un événement qui sort du cadre des mathématiques...
par b.... il se produit un événement qui sort du cadre des mathématiques...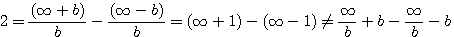
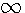 par b la relation devient fausse, elle reste égale à 2b.
par b la relation devient fausse, elle reste égale à 2b. 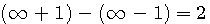
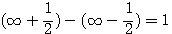
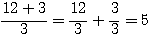
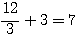 et
et 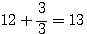 tout deux différents de 5.
tout deux différents de 5.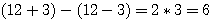
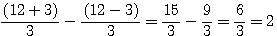
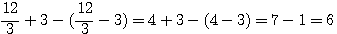
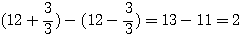
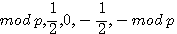
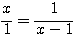 , qui abouti en faisant le produit en croix à
, qui abouti en faisant le produit en croix à 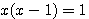
 l'une des solutions de cette équation du second degrés est :
l'une des solutions de cette équation du second degrés est : 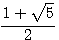 .
.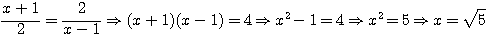
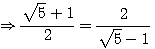
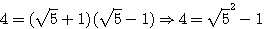
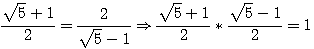

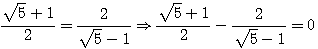
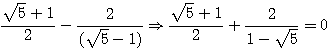
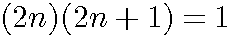
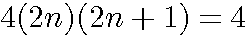
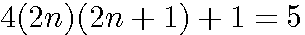
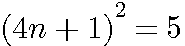
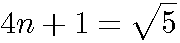
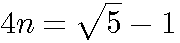
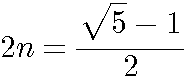
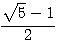
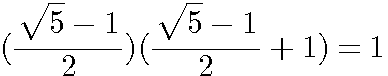
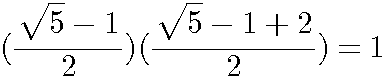
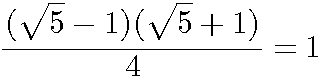
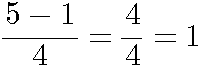
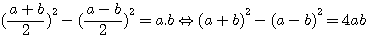 .
.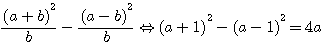 ,
, 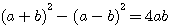
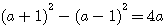
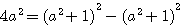
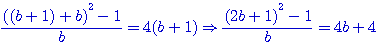
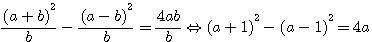
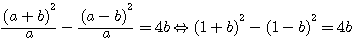
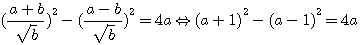
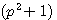
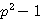 .
.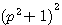 ,
,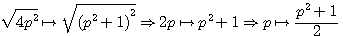 , le deuxième coté étant égal à
, le deuxième coté étant égal à 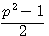
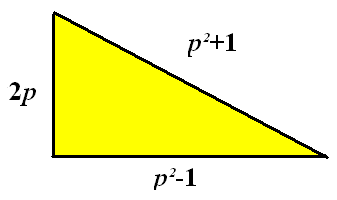
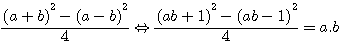
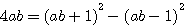 et si
et si 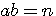 alors
alors