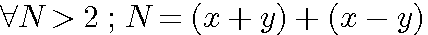L'Axiome de Diophante (*)
A partir de bon nombres de question de l'Arithmética et plus particulièrement de la question 30 du livre 1 , j'en ai extrait une autre question plus simple , qui aurait du être la première question.
(*)Axiome : Equation tellement evidente qu'elle n'a pas besoin d'être prouvée
Livre 1 question 0
On donne une somme et une différence de deux nombres, trouver ces 2 nombres
Exemple: Si je vous donne 13 est une somme de deux nombres et 5 une différence de ces deux même nombres alors :
13 = (9+4) et 5 = (9-4)
Livre 1 Question 30
On donne la somme et le produit de deux nombres : trouver ces deux nombres.
Comment trouver ces deux nombres ?
Soit S = une somme et D une différence il existe un nombre A = S+D et B = S -D
Dans notre exemple: S=13 , D=5 donc A=13+5 = 18 et B=13-5 = 8
|
S=(x+y) et D=(x-y) |
|
|
A=S+D |
B=S-D |
|
A=(x+y)+(x-y) |
B=(x+y)-(x-y) |
Trouver X et Y
Trouver X |
Trouver Y |
|
A = S+D = (x+y)+(x-y)
Enlevons les parenthèses S+D=x+y+x-y
les "Y" s"annulent x + x = 2x
S+D=2x
|
B = S-D = (x+y)-(x-y)
Enlevons les parenthèses S-D=x+y-x+y
les "X" s"annulent y + y = 2y
S-D=2y
|
|
|
|
Donc si je reprend mon exemple 13 une somme, 5 une différence alors : X=(13+5)/2 = 9 ,Y(13-5)/2 = 4
Autre exemple : 5 est une somme 4 une différence : x=9/2 y=1/2 => S=(9/2+1/2)/2=5 D= (9/2-1/2)/2=4
L'axiome de Diophante
A partir de la question 0 l'on s'aperçoit que l'on peut affirmer que:
|
Tout nombre entier
S est la somme de 2 nombres : x+y D est la différence de ces 2 MEME nombres : x-y donc : |
important :
D ![]() 0 si x<>y
0 si x<>y
Pourquoi N>2
Si N=1 alors x=y=1/2
N= S+D
S= (1/2 + 1/2) + D = 1+0
SI N=2 alors x=y=1
N= S+D
S=(1+1) + (1-1) = 2+0
Exemples
4=3+1
x=(3+1)/2 =2 y=(3-1)/2=1
4=(2+1)+(2-1)
13=9+4
X=13/2 Y=5/2
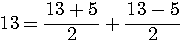


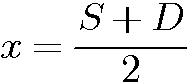 ou 2x = S+D
ou 2x = S+D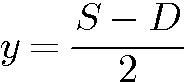 ou 2y=S-D
ou 2y=S-D