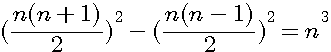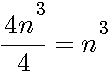Dans la proposition 27 de son deuxième livre , Claude-Gaspard Bachet (Mathématicien contemporain de Pierre de Fermat) explique:
Dans la progression arithmétique des nombres impairs , 1,3,5,7, L'unité est le premier cube, la somme des deux impairs suivants le second cube ; la somme des trois impairs suivants le troisième cube ; la somme des quatre impairs suivants , le quatrième cube , etc , à l'infini
|
n |
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
|
2n-1 |
1 |
3 |
5 |
7 |
9 |
11 | 13 | 15 | 17 | 19 | 21 | 23 | 25 | 27 | 29 |
|
1 |
3+5 |
7+9+11 |
13+15+17+19 |
21+23+25+27+29 |
|||||||||||
|
|
13 | 23=8 | 33=27 | 43=64 | 53=125 | ||||||||||
|
TC(n)=n² |
1 |
4 |
9 |
16 | 25 | 36 | 49 | 64 | 81 | 100 | 121 | 144 | 169 | 196 | 225 |
Ligne 2n-1 : nombres impairs de rang n . Exemple si n=4 le 4iéme nombre impair est 7 <=> 2x4-1
Ligne n3 : Théorie de Claude-Gaspard Bachet (Voir ci-dessous) 1=13 , 23=3+5 , 33= 7+9+11
Ligne n² : = la somme des nombres impairs de 1 à n : Exemple si n=4 ,TC(4)= 1+3+5+7 = n² = 16
Bachet explique que le 1er nombre impair est le 1er cube (n=1=n3), la somme des 2 suivants le deuxième cube (3+5=23), la somme des trois suivants 33 , (7+9+11=27=33)...
Par ce moyen comment trouver un cube ? , il faut trouver le rang du premier impair à additionner et du dernier terme où arrêter cette somme...
Hors, la somme totale des termes de l'addition des nombres impairs correspond à un carré ( n² sur le tableau).
Donc , au lieu de prendre la somme des nombres impairs d'un certain rang à un autre, il suffit de prendre la somme totale des nombres impairs jusqu'au plus grand terme , moins la somme totale de 1 jusqu'au plus petit terme.
Ce qui correspond dans les nombres triangulaires carré à un certain carré moins un autre carré.
Exemple : le cube de 4 (égal à 13+15+17+19) est aussi égal à 10² (=1+3+5+...19) - 6² (=1+3+5+...11)=64=43
Comment trouver ces deux carrés ?
Le rang du plus grand carré est égal à une certaine somme des nombres impairs jusqu'à ce plus grand carré = TC(sup) .
Exemple : 53 (souligné dans le tableau ci-dessus) , pour trouver le nombres de nombres impairs qu'il faut pour arriver jusqu'à ce plus grand carré = TC(sup).
Il faut ajouter 1 nombre impair = 13 + les 2 impairs suivants = 23 + les 3 nombres impairs suivants = 33 + les 4 impairs suivants pour 43 et les 5 impairs suivants pour 53. ce qui fait 1 impair + 2 impairs suivants +3 +4+5 =15 nombres impairs <=> la somme de 15 nombres impairs =TC(15) = 15².
T(5)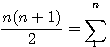 
pour n=5
Dans notre exemple le plus grand carré sera donc égal à la somme de 5(5+1)/2 = 15 nombres impairs = 15²
Même raisonnement pour le plus petit carré qui sera égal à la somme de 4(4+1)/2 = 10 nombres impairs = 10²
Le nombre d'impairs qu'il faut pour ce petit carré est aussi égal à
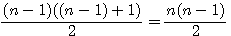pour n=5
Dans l'exemple 53 = 15²-10²
|
TC[T(n)]-TC[T(n-1)] = n3 Ce que nous notons sous la forme arithmétique suivante
|
Preuve que la conjecture des cubes de Claude-Gaspard Bachet est un théorème
Grace à mes précédentes observations et déductions , il s'agit maintenant de prouver mathématiquement mes dires !
Si 
Distribution du carré au dénominateur et diviseur
Double développements de (n+1)² et (n-1)²:
Distribution de n² dans les 2 termes
Dans le deuxième terme -[n4-2n3+n2] on enlève les parenthèses
|
|
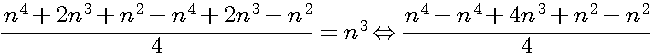
