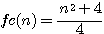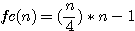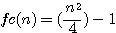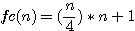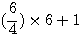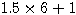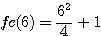|
|

|

En lisant la phrase de Fermat expliquant que sa marge était trop petite pour donner l'explication de sa conjecture (en lisant ses écrits, l'on s'aperçoit qu'il était coutumier du fait), j'ai fondé l'hypothése que Fermat voulait physiquement augmenter la taille de sa feuille.
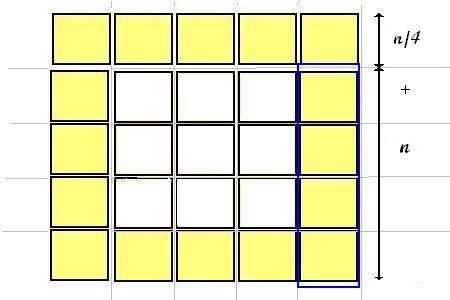
J'ai donc pris un carré de papier et ai procédé au découpage ci-contre.
Division simple à partir d'un carré pair multiple de 4 |
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
|
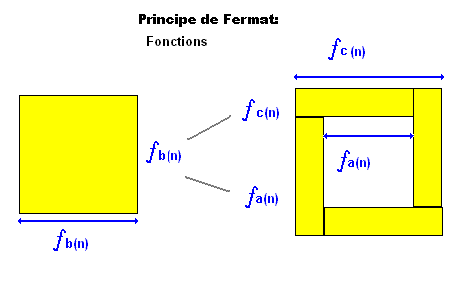
Il sagit de former un carré divisible en 4 bandes , puis les ré-assembler.
Matrice:
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
N=6 ou impair * npair exemple n=6:
9+1 ou
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||

-Patrick Stoltz Dépot INPI N° 343319
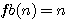
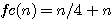
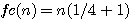
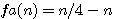
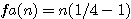
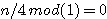
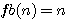
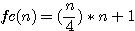
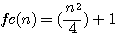 ou
ou