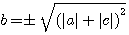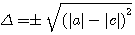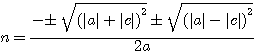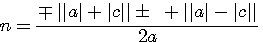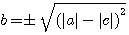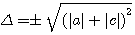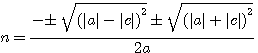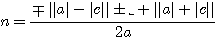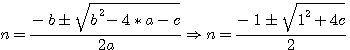Définition:
Une équation literale telle que nous les utilisons communement tout les jours à la forme ax=b. Par exemple si 5 jeans coûtent 50 € , j'écris 5(jean)=50 , 1(jean)=50/5 =10 €. (x=jean) => 1(x)=10€
Cette expression littérale ax=b implique aussi que ax-b=0 , dans mon exemple si je paye pour 5 jeans 50 € il me sera rendu 0€ => 5(10)-50=0
L'équation de forme ax+b=0 est dite du Premier degrés
Par extension , une équation du second degrés à la forme ax²+bx+c = 0 , 3éme degrés = ax3+bx2+cx+d=0 et ainsi de suite
Un peu d'histoire.
Pourquoi une formule aussi compliquée que l'équations du second degrés apparaît dans ce site dédié aux recherches de Diophante et Fermat ?
Alors que Diophante ,ayant vécu entre le Ier-3em siècle, ne disposait même pas des expressions littérales ,celles ci ètants abordées pour la première fois par François Viéte (avocat de son état) fin XVIème siècle !!!
Et pourtant ...
Euclide (3éme Siècle avant JC) défini , avec le nombre d'Or , une première forme simple d'une équation du second degrés => x²-x-1 = 0 est une équation du second degrés , ax²+bx+c=0 pour a=1 , b= -1 , c=-1
Saluons au passage le genie méconnu qu'est Fançois Viéte ; Imaginez faire des mathématiques sans expression littérale !!! Examinons par exemple la définition du nombre d'or faite par Euclide: Une droite et dite divisée en moyenne et extrême raison quand la longueur totale de la droite est à la grande partie ce que cette dernière est à la petite partie !!!
Dans le livre de Diophante dédié aux nombres polygonaux (dont il ne reste que quelques fragments) , Diophante utilise abondamment les équations du second degrés et rapproche les nombres polygonaux, les progressions arithmétiques et les équations du second degrés
Quand à Fermat (XVIIéme Siècle) , disposant lui des expressions littérales il put "finir le travail" de Diophante
Nombre d'or
Démonstration de l'équation du 2ème degrés
|
multiplication de tous les termes par a
factorisation des 2 termes de gauche par an
multiplication par 4
Soit : 4xy=(x+y)²-(x-y)² si x=an et y=(an+b) 4an(an+b) = -4ac <=> (an+an+b)²-(an-(an+b))² ou (an+an+b)²-((an+b)-an)² =
afin de simplifier : (+/-b)² = b²
Comme vu précédemment :
et pour finir
|
Vidéo Youtubes sur le sujet : Vidéo en 3 parties sur les équations du second degrés: 1/ Définitions des équations 2/ 1:46 Démonstration simple des équations du second degrés 3/ 4:50 Histoire des équations |
|
|
b²-4ac est appelé le discriminant, et représenté par la lettre Grécque
|
Obtenir 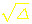 entier selon les signes a,b,c
entier selon les signes a,b,c
Créer un discriminant égal à un carré pour a et c positif
|
Si vous voulez créer une équation du second degrés dont le résultat n soit un nombre entier ou factionnaire il faut que
Comment faire?...observez bien ...
b²- [4ac] = b²-[(a+c)²-(a-c)²] => b²-(a+c)²+(a-c)²
Donc si Plus simplement : 4ac = (a+c)² - (a-c)² <=> (a-c)² = (a+c)² - 4ac
|
Rappel : 4xy = (x+y)² - (x-y)²
4xy=x²+2xy+y²-(x²-2xy+y²)
4xy=x²+2xy+y²-x²+2xy-y²
les x² et y² disparaissent 4xy=+2xy+2xy |
Avec cette relation , en connaissant seulement a , b ou c , nous pouvons générer une infinité d'équation du second degrés entière ou fractionnaire...
Exemple si c = +10 , je choisi b = 3+10=> 3n² + 13n + 10 => 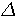 =49
=49
Pour tester vos résultats cet excellent site : https://calculis.net/resoudre-equation-second-degre
(*) outre les differences de signes (développées ci-dessous) , 4ac = 4*a*c mais aussi 4*1*(ac) , si a ou c pair =4*(1/2a) *(2c) etc etc....
Créer un discriminant égal à un carré pour tout signes de a,b,c
+4ac=(a+c)²- (a-c)² x-1 = - 4ac = - (a+c)² + (a-c)² Peu importe c>a ou a>c puisque (a-c)² <=> + 4ac + (a-c)² = (a+c)² (a+c)² -(a-c)² + (a-c)² = (a+c)²
x-1 = - 4ac - (a-c)² = - (a+c)² -4ac+(a+c)²=(a-c)² - (a+c)² + (a-c)² - (a-c)² = - (a+c)²
|
Pour être plus précis ,et rendre plus compréhensif ce qui suit , quand je parle du signe de a ou c, je considère a ou c comme + ou - la valeur absolue de a ou c que l'on note |a| ou |c| donc +a = +|a| , -a = -|a| . (d'autant plus que ni Diophante ou Fermat ne connaissaient les nombres négatifs en tant que tel) Soit b² - [4 * +ac] , puisque + a * + c = +ac ou - a * - c = +ac. si Exemple a et c du même signe + : +3n² + 10n + 7 , a=3 b=10 ,c=7=> (a-c)² = (|7|-|3|)² = 4² Exemple a et c négatifs : - |3|n² + |10| n - |7| , avec l'"ancienne méthode" :
Soit puisque +a * -c = -ac ou -a *+c . -[-4ac] = + 4ac. Dans ce cas ce n'est pas (a+c)² - 4ac = (a-c)² mais (a-c)² + 4ac = (a+c)² b² = (a - c)² => Exemple a et c de signe différents : - |7|n² - |4|n + |3| |
en résumé : Soit 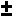 |a|n²
|a|n² 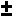 |b|n
|b|n 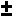 |c| =>
|c| => 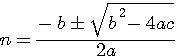 =>
=>
|
a et c sont du même signe : => |
|||
|
b² = (|a|+|c|)²
|
|
|
|
|
a et c sont de signes différents : => |
|||
|
b² = (|a|-|c|)²
|
|
|
|
En résumé
Une des manières de générer une équation du second degrés avec 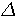 entier: Soit an²+bn+c = 0
entier: Soit an²+bn+c = 0
|
a et c sont du même signe : |
b= a+c |
|
|
a et c sont de signes différents : |
b= a-c |
|
Equation second degrés et équation dite "Diophantesque"
Une expression de la forme n(n+1) est dite "Diophantesque". Elle représente le produit de 2 nombres consécutifs , un nombre dit "oblong" = à la somme des nombre pairs de 1 à n et un double nombre triangulaire. Pour plus de détails , voir la page de ce site sur les nombres polygonaux
Soit le produit de 2 nombres consécutifs trouver ces 2 nombres:
|
Soit l'équation n(n+1)=c alors => n² + n =c => 1n² + 1n -c =0
|
Soit le produit n(n+1)=c
|
Exemple c=30 , 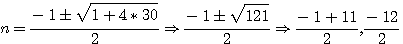 => n=5 ou -6. => 5(5+1)=30 et aussi -6(-6+1) = 30
=> n=5 ou -6. => 5(5+1)=30 et aussi -6(-6+1) = 30

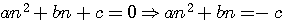
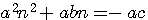
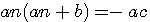
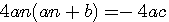
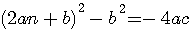
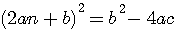
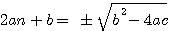
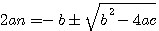
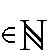 si b²= (a+c)²
si b²= (a+c)²