Introduction
En informatique (dans le langage machine des microprocesseurs) nous avons absolument besoin d'une méthode binaire particulière nommée "Complément à deux" pour pouvoir symboliser les nombres positifs et négatifs et réaliser des opérations
Cette méthode consiste à inverser les bits (NOT) et à ajouter 1
Rappel du binaire
Un bit
Soit un interrupteur qui allume ou pas une ampoule , si celle ci est allumée alors l'on dit que son état = 1 si éteinte son état = 0. Dans mon exemple ,l'état de mon ampoule = un bit
Un digit
Un digit est un groupement de 4 bits , dans l'exemple précédent c'est un alignement indépendant de 4 interrupteurs / ampoules donnant 16 combinaisons d'ampoules allumées/éteintes (24) différentes ..
Le digit est utilisé entre autre pour la numération héxadécimale (compte de 0 à 15)
Pour une représentation binaire plus courte et se note 0x..
Pour les afficheurs numériques digitaux.
Un digit en Héxadécimal
Un octet
Un octet est un groupement de 8 bits , dans mon exemple c'est un alignement indépendant de 8 interrupteurs / ampoules = 28 = 256 combinaisons
système de numération binaire = numération base 2
Soit E un état = 1 pour allumé , 0 = éteint , N = E*20 + E*21 + E*22 + E*23 ...
Tout système de numération se lit de droite à gauche exemple 123 = 3 unités + 2 dizaine + 1 centaine.
Par exemple N=5 sera représenté par le digit 0101 (0x5 en héxa) :
|
|
23=8 |
22=4 |
21=2 |
20=1 |
|
x |
x |
x |
x |
|
|
0 |
1 |
0 |
1 |
|
|
= |
= |
= |
= |
|
|
0 |
+ 4 |
+ 0 |
+1 |
Un digit en binaire :
Représentation d'un négatif en Complément à 1 (instruction NOT)
Le bit de négation
Pour représenter un nombre binaire en nombre positif ou négatif , selon le processeur :
ou on utilise le bit le plus à gauche pour indiquer le signe.
ou on utilise un drapeau (un bit particulier du processeur)
Si l'état de ce bit = 0 alors le nombre est positif
Si l'état de ce bit = 1 alors le nombre est positif
Representation en complément à 1
En complement à 1 il suffit de réaliser un NOT (Traduire PAS en français) de chaque bit.
En booléen NOT (N) se note :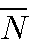 
(rien à voir avec les classes de l'arithmétique modulaire)
Inconvénient de l'addition d'un nombre en complément à 1
En mathématique , si l'on ajoute un nombre et son opposé l'on obtient zéro. (+n)+(-n)=0
En binaire "complément à 1" si l'on ajoute un nombre et son complément à 1 l'on obtient 1111
|
Addition ADD de +5 et -5 en complément à 1 |
||||
|
+5 |
0 |
1 |
0 |
1 |
|
+ |
+ |
+ |
+ |
|
|
NOT 5 |
1 |
0 |
1 |
0 |
|
= |
1 |
1 |
1 |
1 |
1111 serrait la representation de quoi ? Pas -1 puisque NOT 0001 donne 1110 donc 1111 donne -0.
On pourrait s'en contenter sauf que quand l'on compte de -1 à 1 l'on obtient -1 , 0, 1 et non pas -1,-0,+0,+1 !!!!
Instruction booléenne:NOT
Not = inversion des 0 et des 1
un 1 devient 0 et vise versa.
Table de vérité pour 1 bit
|
1 |
0 |
|
|
NOT = |
0 |
1 |
Exemple N=+5
|
NEG |
22=4 |
21=2 |
20=1 |
|
0 |
1 |
0 |
1 |
|
NOT => -5 en complément à 1 |
|||
|
1 |
0 |
1 |
0 |
N=0
|
NEG |
22=4 |
21=2 |
20=1 |
|
0 |
0 |
0 |
0 |
|
avec le complément à 1 NOT 0 => 1111 |
|||
|
1 |
1 |
1 |
1 |
Complément à 2 (instruction NEG processeur 8086/8088)
Pour palier à l'inconvénient expliqué ci dessus , on ajoute 1 à son complément à 1.
|
-N = |
Exemple de +5 = 0101 transformé en -5 avec le complément à deux :
|
Rang |
signe - |
22=4 |
21=2 |
20=1 |
|
5 |
0 |
1 |
0 |
1 |
|
not 5 |
1 |
0 |
1 |
0 |
|
+1 |
1 |
0 |
1 |
1 |
Ce qui donne -5 = 1011
Le complément à 2 de 0 est égal à 1111 + 1 = 0
(*)ligne +C = Retenue : La retenue en binaire (Carry en anglais) fonctionne de la même manière qu'en arithmétique C.A.D dans la vérification de l'exemple pour le 1er bit (à droite) 1+1 = 0 retenue 1 reportée sur le 2ème bit: 0+1+ 1 de retenue = 1 ...
Vérification (+5) + (-5) = 0
En addition bit à bit :
|
5 |
0 |
1 |
0 |
1 |
|
|
+ -5 |
1 |
0 |
1 |
1 |
|
|
(*) +C= retenue |
1 |
1 |
1 |
1 |
0 |
|
= |
0 |
0 |
0 |
0 |
|
Processeurs 6502 / 8x86
ADD Add without carry
La retenue C n'est pas reportée pour l'octet suivant
ADC add with carry
La retenue C est reportée pour l'octet suivant
Résumé
Complément à deux et incrémentation
Si l'on décrémente 0001 l'on obtient 0 (1-1 = 0) , si l'on incremente 0111= 7 l'on obtient 1000 CAD -0
Idem pour les négatifs : la représentation en complément à 2 de 0111=7 nous donne 1001=-7 décrémenter de 1 -> 1000 CAD -0
-1 en complément à 2 = 1111 (0001->1110+1=1111) +1 est bien égal à 0
Selon le sens de l'opération l'on obtient -0 ou +0
Playlist Youtubes sur le sujet
Dans les vidéos ci-dessous outre l'écart de 2 à chaque marche, si je me situe entre la marche -1 et +1 alors la marche 0 à une réalité physique différente de rien.
En binaire,le 0 à aussi un état physique: C'est le complément à un. Il faut ajouter aussi le fait qu'en binaire chaque bit à 2 états , c'est le complément à deux.
Cliquez sur 
ci dessous pour afficher la liste des vidéos
Autres pages d'applications informatiques
Rubriques principales du site
