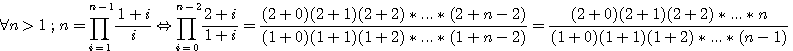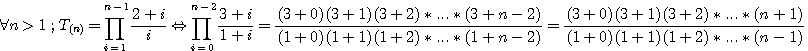|
Notes sur "Clef de Fermat" Correspondance de cette formule et les nombre polygonaux
Si nous voulons inclure 1 dans la sequence du numérateur ( 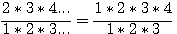 ) ; si n=2 alors ) ; si n=2 alors 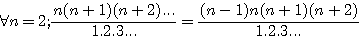
Exemple 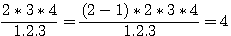
Je vous rappelle que la formule des nombres polygonaux est 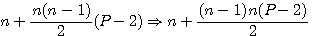 ( P = le nombre de cotés du polygone ) , nous commençons à entrevoir la correspondance entre les nombres polygonaux et leurs cotés... ( P = le nombre de cotés du polygone ) , nous commençons à entrevoir la correspondance entre les nombres polygonaux et leurs cotés...
Notes sur "Clef de Fermat" Recherche de triangulaires / dénominateur commun
Soit a = 14 réalisons un tableau de sa factorielle :
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
et le Triangulaire juste inférieur à 14 , c'est à dire 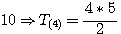 et réalisons aussi sa factorielle par et réalisons aussi sa factorielle par 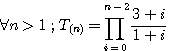
Démonstration compliquée (Conseil
Pour soustraire la deuxième factorielle de la première , comme bon collégien , il faut mettre la deuxième factorielle au même dénominateur (n-1!) en multipliant en haut et en bas par 4*5*6*7*8*9*10*11*12*13 donc:
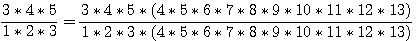 (ouf ! ...lol) (ouf ! ...lol)
Pour réaliser la soustraction: 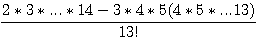 il faut regrouper les facteurs communs des deux termes, puis factoriser et soustraire : il faut regrouper les facteurs communs des deux termes, puis factoriser et soustraire :
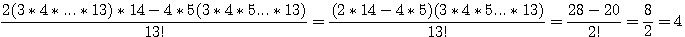
Nota : Soit 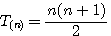 , ce deuxième nombre ne peut être supérieur à n (dans cet exemple il est égal) sinon il serait = à n+1 et serait un triangulaire supérieur. , ce deuxième nombre ne peut être supérieur à n (dans cet exemple il est égal) sinon il serait = à n+1 et serait un triangulaire supérieur.
Réalisons une nouvelle itération pour 4 , le triangulaire inférieur étant 3 alors :
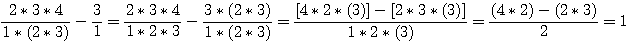 ; Donc 14 = 10+3+1 = ; Donc 14 = 10+3+1 =  (4) + (4) +  (2) + (2) +  (1) (1)
Vous me dirai que cela fonctionne par ce que le nombre choisi 14 -  (4) est relativement petit (dans l'exemple 14-10 =4) , donc généralisons cette itération pour vérifier. (4) est relativement petit (dans l'exemple 14-10 =4) , donc généralisons cette itération pour vérifier.
Premier écart entre un nombre n = 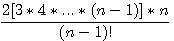 et et 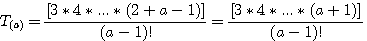 ; les nombres indiqués dans cette formule (2,3,4 ) sont des constantes ; les nombres indiqués dans cette formule (2,3,4 ) sont des constantes
Mise de  (a) au même dénominateur que n: Etant donné que diviseur du triangulaire (a) au même dénominateur que n: Etant donné que diviseur du triangulaire  (a) = 1 x 2 x .... x(a-1) Il faut multiplier le diviseur de a jusqu'a (n-1) => a x a+1 x ...x (n-1) ; et par consequent aussi le numérateur : (a) = 1 x 2 x .... x(a-1) Il faut multiplier le diviseur de a jusqu'a (n-1) => a x a+1 x ...x (n-1) ; et par consequent aussi le numérateur : 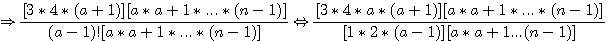 . .
Dans la séquence du numérateur : 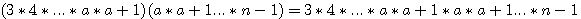 ,la séquence ,la séquence 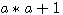 se répète deux fois donc : se répète deux fois donc : 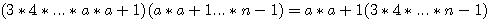
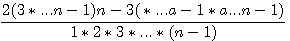
Vérification : Les éléments communs des deux numérateurs et du dénominateur commun sont 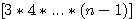 et les facteurs différents sont : 2*n et a*a+1 et les facteurs différents sont : 2*n et a*a+1
Ce qui donne bien après simplification cet écart entre n et  (a) : (a) : 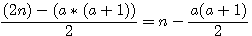
Mais cette démonstration N'ABOUTI QU'A UN SIMPLE VERIFICATION
1/ Recherche d'un triangulaire contenu dans n par le "crible de Fermat"
....que tout nombre est triangulaire ou composé de deux ou de trois triangulaires...
Afin de trouver un triangulaire contenu dans un nombre , j'ai fait une première recherche par les dénominateurs communs entre 2 triangulaires (sur ce lien (dans mes notes perso) , qui n'abouti qu'a une vérification de  . .
Il existe un moyen beaucoup plus simple, qui va vous paraître au premier abord très empirique, pour trouver le plus grand nombre triangulaire contenu dans un nombre (nous verrons par la suite que plusieurs triangulaires sont possible ... ) . Ce moyen nous est indiqué par Fermat dans sa note du 4 Novembre 1636 (à Roberval) où Fermat exprime le quadruple du triangulo-triangulaire par la formule  ,J'avais observé (sur la page des nombres polygonaux) que si le diviseur était égal à 1.2.3.4, et que je supprime le .4 (. est le signe pour la multiplication utilisé par Fermat) , ce nombre est bien le quadruple de ,J'avais observé (sur la page des nombres polygonaux) que si le diviseur était égal à 1.2.3.4, et que je supprime le .4 (. est le signe pour la multiplication utilisé par Fermat) , ce nombre est bien le quadruple de 

Prenons maintenant la factorisation de 14 par  et positionnons la série de facteurs de 14 dans un tableau: et positionnons la série de facteurs de 14 dans un tableau:
:
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
=14 |
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
Par le même moyen que nous avons utilisé pour rechercher le coté d'un triangulaire (Rappel par l'exemple ci-dessous ou en détail sur ce lien )
Si  (5) = 15 alors (5) = 15 alors 
Trouvons le triangulaire contenu dans le nombre 14
La série de fractions de  est : est :
|
 (2)= (2)=
|
x |
=  (3) (3)
|
x |
=  (4) (4)
|
x |
=  (5) (5)
|
x... |
(pour n>1)  (n) (n)
|
| 3 |
4 |
5 |
6 |
n+1 |
| / |
/ |
/ |
/ |
/ |
| 1 |
2 |
3 |
4 |
n-1 |
|
<=>
2*3/2=3
|
|
<=>
3*4/2=6
|
|
<=>
4*5/2=10
|
|
|
|
|
Si , dans le tableau de n , je raye le nombre 3 du numérateur alors:
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
=
|
14
/
3
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
et je raye le nombre 1 du dénominateur alors :
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
=
|
14*1
/
3
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
Cela revient à multiplier par l'inverse du premier triangulaire , =14* (1/3) =14/3. Dans ce résultat 14 > 3 => le résultat de cette division sera > 1.
Le résultat de la division Euclidienne => 14/3 = 4 reste 2 ) ,Recommençons avec le triangulaire +1
Rayons le nombre 4 du numérateur et le nombre 2 du dénominateur alors :
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
=
|
14*2
/
(3*4=12)
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
=28/12 > 1 (= 2 reste 4) , nous recommençons l'itération
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
14
|
=
|
28*3=84
/
(12*5)=60
|
|
1
|
2
|
3
|
4
|
5
|
6
|
7
|
8
|
9
|
10
|
11
|
12
|
13
|
= 84>60 (=1 reste 24) si je continu (étant donné le résultat de la division ) le numérateur deviendra inférieur au numérateur (= 84*4/60*6=336/360)
Pour trouver le triangulaire contenu dans n (14 dans l'exemple ) Nous avons donc multiplié successivement l'inverse des facteurs d'un nombre triangulaire de la formule  c'est à dire c'est à dire  jusqu'à obtenir 1 , le plus grand triangulaire possible (*) plus un reste... jusqu'à obtenir 1 , le plus grand triangulaire possible (*) plus un reste...
(*) Nous verrons par la suite qu'il peut exister plusieurs triangulaire possible , mais qu'un seul abouti à trouver le moins de triangulaires possible contenu dans n...
Nous obtenons donc l' inverse du triangulaire contenu dans n multiplié par ce nombre ,  , plus généralement : , plus généralement : 
Puisqu'un des deux diviseurs est divisible par 2 ,alors divisons un des deux et "rayons" 2 du numérateur 
Nous calculons  = 1 reste 4 égal aussi au numérateur-diviseur = 14-10=4 = 1 reste 4 égal aussi au numérateur-diviseur = 14-10=4
Recherche des triangulaires contenus dans 4 :
|
2
|
3
|
4
|
=>
|
2
|
3
|
4
|
=> |
8
/
6
|
|
1
|
2
|
3
|
1
|
2
|
3
|
4 - 3 = 1 , Donc 14 = 10+3+1 =  (4) + (4) +  (2) + (2) +  (1) . Grâce à ce moyen nous nous somme passé des dénominateurs communs (de cette démonstration) (1) . Grâce à ce moyen nous nous somme passé des dénominateurs communs (de cette démonstration)
Nombres triangulaires et arithmétique modulaire.
|
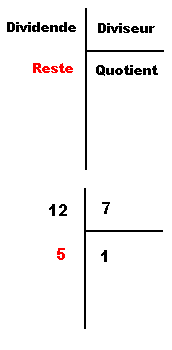
Grâce à cet algorithme , j'ai réussi à prouver et à vous "faire avaler" que 14-10 = 4 = 14/10 ... Étonnant non ? Et pourtant si le quotient d'une division = 1 alors une division égale une soustraction . Sur l'exemple ci - contre , 12-7 = 5 équivaut au reste de 12/7 =5
D'ou aussi dans la recherche du PGCD entre 2 nombres , il existe 2 algorithmes : soustractions successives ou diviseur / division / reste.
C'est le principe même de l'arithmétique modulaire. si le quotient = 1 alors Dividende - diviseur = Dividende  reste (mod Diviseur) reste (mod Diviseur)
Dans l'exemple donc , 14/10 = 10/10 + 4/10 = 1 + 4/10 , dans 4/10 nous avons 4 au numérateur n'excédant pas le premier triangulaire trouvé par le "crible de Fermat" représenté par le dénominateur (Fermat et Diophante dirait "mesuré par un triangulaire) ; 4 est < à 14
En fait ,par ce moyen , nous ne trouvons pas le plus grand triangulaire contenu dans n , mais le premier triangulaire dont le reste ne dépasse pas ce triangulaire (peut être égal , par exemple pour 20 = 20/10 = 10/10 + 10/10)
 Important : si (dans l'exemple) 28/20 est arithmétiquement égal à 14/10 , dans l'arithmétique modulaire ce n'est pas vrai : Important : si (dans l'exemple) 28/20 est arithmétiquement égal à 14/10 , dans l'arithmétique modulaire ce n'est pas vrai :
20/28 = 1 reste 8 alors que 14/10 = 1 reste 4
 Je note Je note 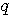 le quotient de la division Euclidienne différent de le quotient de la division Euclidienne différent de  , coefficient qui multiplie les 4 opérateurs d'une division , coefficient qui multiplie les 4 opérateurs d'une division
|
|
Inverse d'un triangulaire:
Réaliser un "Crible de Fermat" paraît fastidieux et empirique mais j'ai détaillé ce mécanisme pour vous montrer qu'en fait, pour trouver un triangulaire tel que n /  (a) =1 + reste, nous avons multiplié n par l'inverse d'un triangulaire. Quand nous avons "criblé" 14 pour trouver le premier Triangulaire : (a) =1 + reste, nous avons multiplié n par l'inverse d'un triangulaire. Quand nous avons "criblé" 14 pour trouver le premier Triangulaire :
|
2
|
3
|
4
|
5
|
6
|
7
|
...
|
14
|
|
1
|
2
|
3
|
4
|
5
|
6
|
...
|
13
|
nous avons en fait divisé n=2x3x4x...14/13! par 3x4x5 /3! =>  ;(colonne 3! <=> i=2) inverse que nous trouvons en divisant la première ligne du tableau des "cotés d'un nombre polygonal" (N=1 toujours égal à 1) par la troisième ligne du tableau de la colonne 3! (correspondant à 1*2*3 "rayés" dans le crible. ;(colonne 3! <=> i=2) inverse que nous trouvons en divisant la première ligne du tableau des "cotés d'un nombre polygonal" (N=1 toujours égal à 1) par la troisième ligne du tableau de la colonne 3! (correspondant à 1*2*3 "rayés" dans le crible.
|
1!
|
2!
|
3!
|
4!
|
5!
|
6!
|
7!
|
|
i=0
|
i=1
|
i=2
|
i=3
|
i=4
|
i=5
|
i=6
|
| N=1 |
1
|
1
|
1
|
1
|
1
|
1
|
| N=2 |
3
|
4
|
5
|
6
|
7
|
8
|
| N=3 |
6
|
10
|
15
|
21
|
28
|
36
|
Puis , de nouveau nous avons multiplié le reste de 14/10 c'est à dire 4 par un nouvel inverse : 1/3 =>4/3 = 1 reste 1 , 1 représentant dans ce cas le troisième triangulaire.

|
notation:

La récurrence décrite peut être représentée par:

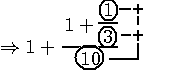
|
Recherche des triangulaires qui composent un nombre :
|
44
|
44
|
44
|
44
|
|
1/T(6)
|
1 / T(7)
|
1 / T(8)
|
1 / T(9)
|
|

|

|

|

|
|
44
/
21
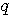 =2 r=2 =2 r=2
|
44
/
28
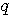 =1 r=16 =1 r=16
|
44
/
36
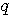 =1 r=8 =1 r=8
|
44
/
45
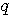 =0 r=45 =0 r=45
|
|
Plusieurs triangulaires possible par un autre exemple : n=44
Si nous recherchons les triangulaires contenus dans 44 tel que 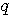 =1 (dans la colonne T de la matrice ci-dessus ), nous trouvons (ci contre) 28 (7*8/2) , et 36 (8*9/2) : =1 (dans la colonne T de la matrice ci-dessus ), nous trouvons (ci contre) 28 (7*8/2) , et 36 (8*9/2) :
Si nous décomposons le reste de 44/28 => r =16 alors nous trouvons deux triangulaires 15 et 3
Si par contre nous décomposons le reste de 44/36 => r = 8 alors nous trouvons 3 autres triangulaires : 6 + 1 + 1
Selon Fermat :
OBS DE FERMAT. Bien plus , j'ai découvert le premier une proposition très belle et très générale, savoir ; que tout nombre est triangulaire ou composé de deux ou de trois triangulaires;...
Tout nombre est composé de 3 Triangulaires maximum , C'est à dire divisible par un Triangulaire , exemple 10 est composé d'un Triangulaire , 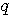 =1 r=0) , par deux Triangulaires (30 est composé de 2*T(6) c'est à dire 2*15 , =1 r=0) , par deux Triangulaires (30 est composé de 2*T(6) c'est à dire 2*15 , 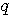 =2 r=0 ) ou par Trois Triangulaires égaux ou non , =2 r=0 ) ou par Trois Triangulaires égaux ou non , 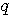 =3 r=0 ou trois récurences maximum =3 r=0 ou trois récurences maximum
|
Introduction de Zéro:
Si nous voulons , pour une meilleure lisibilité, faire coïncider la formule 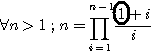 ,et sa factorielle correspondante ,et sa factorielle correspondante 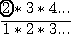 alors nous devons modifier la valeur de alors nous devons modifier la valeur de 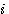 ,qui s'incrémente de 1 à n-1, en 0 à n-2 et compter à partir de zéro 0. (rappel n>1) . ,qui s'incrémente de 1 à n-1, en 0 à n-2 et compter à partir de zéro 0. (rappel n>1) .
Exemple soit le nombre 3 , au lieu de compter 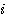 de 1 à 3-1 c'est à dire de 1 à 3-1 c'est à dire 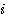 =1 , =1 , 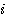 =2 nous comptons =2 nous comptons 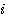 de 0 à 3-2 , c'est à dire de 0 à 3-2 , c'est à dire 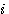 =0, =0, 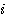 =1 ; le nombre de boucles restant identique. =1 ; le nombre de boucles restant identique.
Autant cette nouvelle formule n'est pas mathématiquement très académique mais est totalement correcte en informatique (for i=0 to n-2 ... au lieu de: for i=1 to n-1 ; Dans la boucle for i=0 to n-2 si n=2 alors la boucle s'effectuera une fois.)
Modifions ainsi cette formule pour un nombre triangulaire  : :
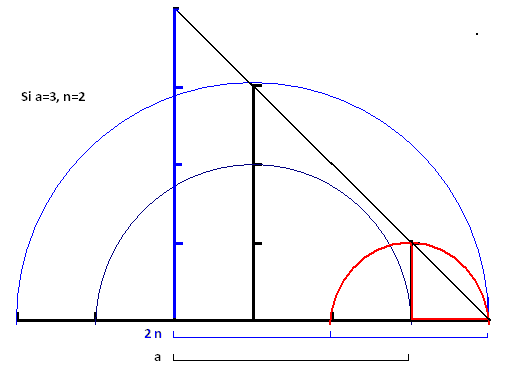
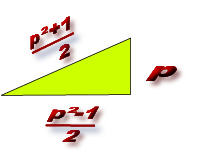
|

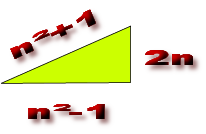
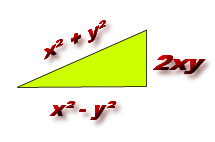
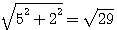 ) est le triangle de base d'un nouveau triangle rectangle ; D'un coté (d+b) = 7 =Y et d'un autre coté (d-b)=3 et d'hypothénuse :
) est le triangle de base d'un nouveau triangle rectangle ; D'un coté (d+b) = 7 =Y et d'un autre coté (d-b)=3 et d'hypothénuse : 
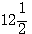 que l'on doit traduire par 12 + 1/2 et non pas 12 multiplié par 1/2) mais 12 multiplié par 5
que l'on doit traduire par 12 + 1/2 et non pas 12 multiplié par 1/2) mais 12 multiplié par 5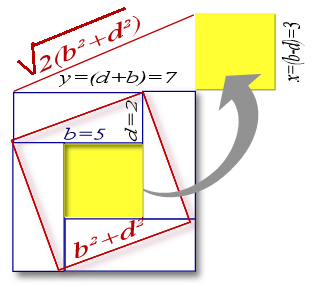
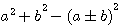
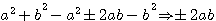 , la différence est + ou - 2ab
, la différence est + ou - 2ab
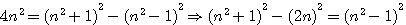
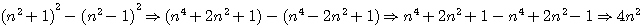
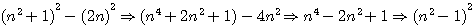
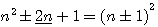
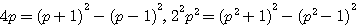 et n'admet qu'une solution..
et n'admet qu'une solution..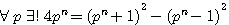
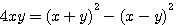 , le couple
, le couple 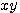 est forcement égal a un seul nombre par 1,(appelé p par la suite).
est forcement égal a un seul nombre par 1,(appelé p par la suite). 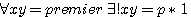
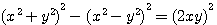 ,pour obtenir un triangle rectangle dont l'hypothènuse² ext égale à x²+y², x*y doit étre au moins divisible par 2 , xy
,pour obtenir un triangle rectangle dont l'hypothènuse² ext égale à x²+y², x*y doit étre au moins divisible par 2 , xy 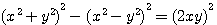 , la surface du triangle rectangle
, la surface du triangle rectangle 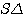 de coté
de coté 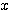 et
et 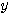 ,(et d'hypothénuse
,(et d'hypothénuse 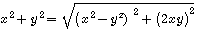 ) est égale à:
) est égale à: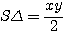
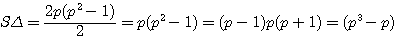

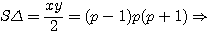
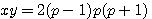
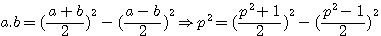 , si ce triangle est rectangle alors
, si ce triangle est rectangle alors 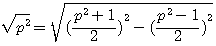 ,
,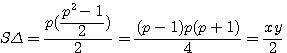 ;qiui aprés produit en croix:
;qiui aprés produit en croix: 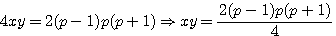
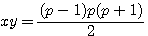
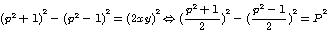
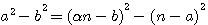 en utilisant la méthode de Fermat :
en utilisant la méthode de Fermat :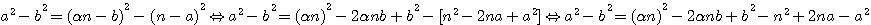
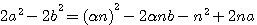
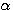 par sa valeur a / b
par sa valeur a / b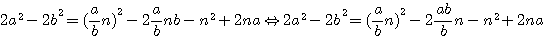
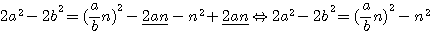
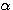 pour éliminer -2
pour éliminer -2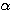 nb et 2na en les égalant à 0
nb et 2na en les égalant à 0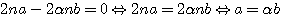
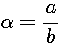
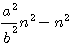
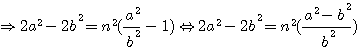 et factorisation du terme
et factorisation du terme 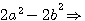
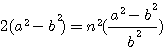
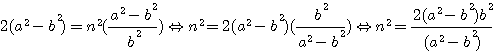
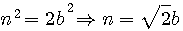
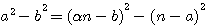 ,
, 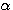 par a/b et n par
par a/b et n par 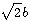
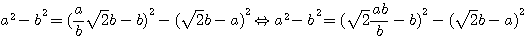
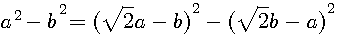
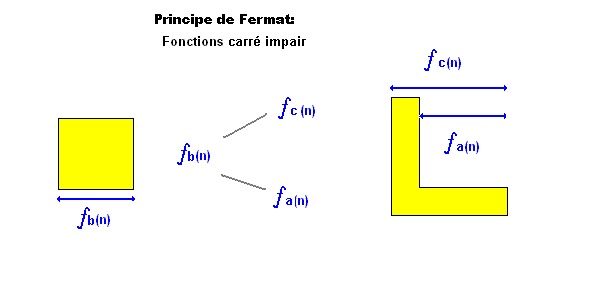
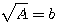
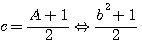 = formule de
= formule de 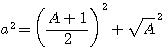
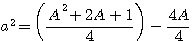
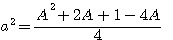
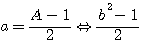 = formule de topologie impaire pour a
= formule de topologie impaire pour a
 =
= 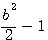 ,
,  =
= 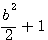
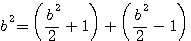
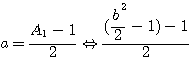
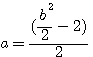 =
=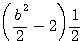
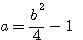 = formule de
= formule de 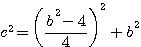
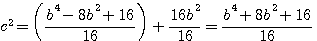
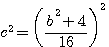 ,
, 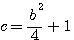
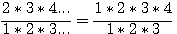 ) ; si n=2 alors
) ; si n=2 alors 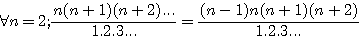
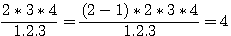
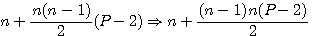 ( P = le nombre de cotés du polygone ) , nous commençons à entrevoir la correspondance entre les nombres polygonaux et leurs cotés...
( P = le nombre de cotés du polygone ) , nous commençons à entrevoir la correspondance entre les nombres polygonaux et leurs cotés...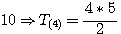 et réalisons aussi sa factorielle par
et réalisons aussi sa factorielle par 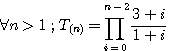
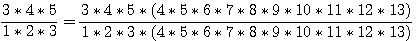 (ouf ! ...lol)
(ouf ! ...lol)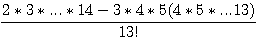 il faut regrouper les facteurs communs des deux termes, puis factoriser et soustraire :
il faut regrouper les facteurs communs des deux termes, puis factoriser et soustraire :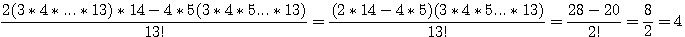
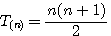 , ce deuxième nombre ne peut être supérieur à n
, ce deuxième nombre ne peut être supérieur à n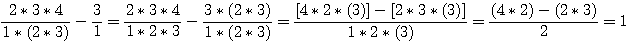 ; Donc 14 = 10+3+1 =
; Donc 14 = 10+3+1 = 
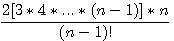 et
et 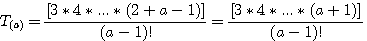
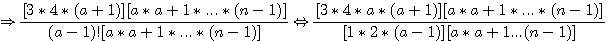 .
.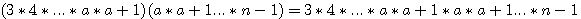 ,la séquence
,la séquence 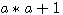 se répète deux fois donc :
se répète deux fois donc : 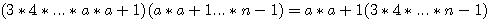
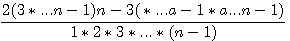
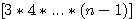 et les facteurs différents sont : 2*n et a*a+1
et les facteurs différents sont : 2*n et a*a+1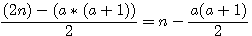
 .
. ,J'avais observé (sur la page des
,J'avais observé (sur la page des 

 et positionnons la série de facteurs de 14 dans un tableau:
et positionnons la série de facteurs de 14 dans un tableau:
 est :
est :  c'est à dire
c'est à dire  jusqu'à obtenir 1 , le plus grand triangulaire possible (*) plus un reste...
jusqu'à obtenir 1 , le plus grand triangulaire possible (*) plus un reste... , plus généralement :
, plus généralement : 

 = 1 reste 4 égal aussi au numérateur-diviseur = 14-10=4
= 1 reste 4 égal aussi au numérateur-diviseur = 14-10=4 , coefficient qui multiplie les 4 opérateurs d'une division
, coefficient qui multiplie les 4 opérateurs d'une division
 ;(colonne 3! <=> i=2) inverse que nous trouvons en divisant la première ligne du tableau des "cotés d'un nombre polygonal" (N=1 toujours égal à 1) par la troisième ligne du tableau de la colonne 3! (correspondant à 1*2*3 "rayés" dans le crible.
;(colonne 3! <=> i=2) inverse que nous trouvons en divisant la première ligne du tableau des "cotés d'un nombre polygonal" (N=1 toujours égal à 1) par la troisième ligne du tableau de la colonne 3! (correspondant à 1*2*3 "rayés" dans le crible.


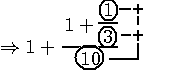




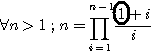 ,et sa factorielle correspondante
,et sa factorielle correspondante 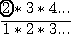 alors nous devons modifier la valeur de
alors nous devons modifier la valeur de 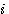 ,qui s'incrémente de 1 à n-1, en 0 à n-2 et compter à partir de zéro 0. (rappel n>1) .
,qui s'incrémente de 1 à n-1, en 0 à n-2 et compter à partir de zéro 0. (rappel n>1) . 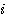 de 1 à 3-1 c'est à dire
de 1 à 3-1 c'est à dire 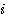 =1 ,
=1 , 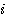 =2 nous comptons
=2 nous comptons 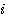 de 0 à 3-2 , c'est à dire
de 0 à 3-2 , c'est à dire 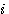 =0,
=0, 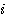 =1 ; le nombre de boucles restant identique.
=1 ; le nombre de boucles restant identique.