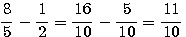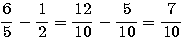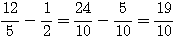Question 31: Trouver quatre carrés qui, ajoutés entre eux et à leurs cotés, fassent un nombre donné

Notez qu'un carré n² + son coté =  n(n+1) est un oblong (somme des nombres pairs) et n(n+1)/2 est un nombre triangulaire (somme des nombres de 1 à n)

Solution, Soit 12 le nombre donné; cherchons quatre carrés qui fassent en somme 12 + 1, de telle sorte qu'on ait a² + b² + c² + d² = 12+1; Cette équation prendra la forme :

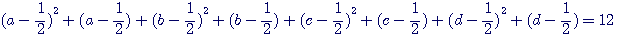
Qui aprés factorisation / développement => 

a²-1/4 + b²-1/4 + c²-1/4 + d²-1/4 = 12

a²+b²+c²+d²-1 = 12 => a²+b²+c²+d² = 12+1=13

Et la question sera résolu si l'on connait a,b,c,d ; or 13 est la somme de deux carrés 4 (=2²) et 9 (=3²)

4 est la somme de deux carrés 8²/5² , 6²/5²

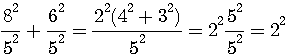
a=8/5 ; b =6/5

9 est la somme des deux carrés 12²/5² et 9²/5²

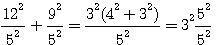
c=12/5 ; d=9/5

Egalité de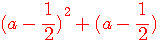

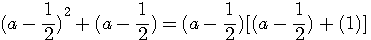
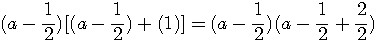
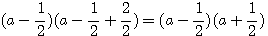
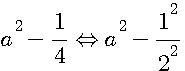
a²=8²/5² , b²=6²/5² , c²=12²/5² , d²= 9²/5² ; a²+b²=2² ; c²+d² = 3² => 2²+3²=13

Les cotés des carrés cherchés seront donc 11/10 , 7/10 ,19/10 ,13/10

a-1/2	b-1/2	c-1/2	d-1/2

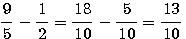OBS de Fermat. Bien plus , j'ai décoouvert le premier une proposition très belle et très générale , savoir ; que tout nombre est triangulaire ou composé de deux ou de trois triangulaire ; carrés ou composé de deux  , de trois ou de quatre carrés ; pentagone ou ou composé de deux  , de trois , de quatre ou de cinq pentagones , et ainsi de suite à l'infini , on peut énoncer cette merveilleuse proposition pour les hexagones, les heptagones , et généralement pour les polygones quelconques, d'aprés le nombre de leurs angles.

Mais il ne convient pas de placer ici sa démonstration qui est déduite de plusieurs mystères les plus variés et les plus abstrus des nombres , car nous avons résolu de destiner à cet objet un Livre complet , et d' étendre merveilleusement dans cette partie l'arithmétrique au delà de ses anciennes limites connues

La formule des nombres polygonaux la plus utilisée est : 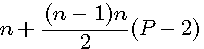      où P est le nombre de cotés du polygone