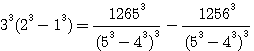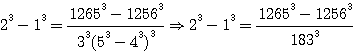|
|
 Arithmetica Diophante / Fermat / Bachet / Brassine Livre IV Question 1 et 2 |
Contacts: |
|
En bleu les annotations de Diophante. |
En marron italique les annotations de Bachet |
En vert les annotations de Fermat. |
En bleu marine Emile Brassine |
|
Sur fond jaune, des notes importantes et les calculs réalisés avec les équations retrouvées avec les nombres donnés en exemple dans les notes de Fermat |
|||
Livre IV,Question I et II Diviser un nombre en deux cubes, dont la somme des cotés est aussi donnée |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Question I Diviser un nombre en deux cubes, dont la somme des cotés est aussi donnée. Solution. Nombre donné 370, nombre des cotés des cubes 10. Un des cubes sera (N+5)3 , l'autre (5-N)3 , leur somme 30N² + 250 = 370 ; d'oû N=2; coté du premier cube 7, cotè du second 3. Details : nota: n+5+5-n=10
|
Question II Trouver deux nombres dont la différence soit égale à un nombre donné, et dont la différence des cubes soit aussi donnée. Solution: différence des nombres 6, Différence de leurs cubes 504. Le premier nombre sera N+3 , le second N-3; la difference de leurs cubes 18N²+54 = 504 , N=5; coté des cubes 8 et 2
Details :
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
Si l'on divise n en deux cubes de coté a (somme des 2 cubes = 2a) et nous l'égalons à D (différence des deux cubes) nous obtenons la formule générale suivante:
|
|
|||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Livre IV,Question II ,Questions supplémentaires de BachetDans le commentaire de la question II; Bachet propose les trois questions suivantes: 1er question: étant donnés deux cubes, en trouver deux autres dont la somme soit égale à la différence des deux premiers.Il faut de plus que le double du petit ne surpasse pas le plus grand. ( 2me question : Étant donnés deux cubes, en trouver deux autres dont la différence égale la somme des cubes donnés ( 3ème question: Étant donné deux cubes, en trouver deux autres dont la différence égale la différence des cubes donnés. le double du plus petit cube doit exeder le plus grand ( |
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
|
OBS DE FERMAT: Nous avons facilement étendu par la répétition de l'opération la détermination de la première question, et nous avons généralement construit cette question et les suivantes, ce que Bachet et Viele lui-même n'avaient accomplir : soient 64 et 125 les deux cubes données, il faut en trouver deux autres dont la somme soit égale à la différence des cubes donnés. Pour la solution à la 3éme question , Bachet trouve que les cubes sont 15252992/250047 et 125/250047 Note de Emile Brassine: Quand on a une relation de la forme a3+b3=x3+y3, a et b étant donnés, il est facile de trouver tout d'abord une solution en posant Cliquez ici pour aller directement à la suite de l'observation de fermat
Si l'on pose directement la première ou la deuxième question de Bachet b3 ne disparaît pas (a3-b3= a3.... +B3...) mais deviens 2b3 ce qui conduit à poser directement la troisième question. selon le modèle du cas particulier de Bachet.
Posons selon la proposition de Fermat, la 3em question en version positive.
Factorisons de ces deux équations et découvrons quelques conjectures étonantes ou cliquez ici pour passer directement à la suite
D'après le mode de determination, ces cubes ont une différence égale à celle des cubes donnés; mais ces deux cubes trouvés par l'opération de la troisième question ( Ainsi étant donnés ces deux cubes , qu'on en cherche deux autres don't la somme soit égale à la différence des cubes donnés, ce qui est permis par la détermination de la question première ( Et voici maintenant , la phase la plus surprenante : Mais la différence des deux cubes trouvés est, d'après la troisième question, égale à la différence des deux cubes considérés d'abord, savoir 64 et 125, par conséquent rien n'empéche de construire deux cubes dont la somme soit égale à la différence des deux cubes donnés 60 et 125, ce qui, sans aucun doute , étonnerait Bachet lui même.. 60 n'etant pas un cube , est ce une faute de frappe ? quelle est cette démonstration qui étonnerait Bachet ? Observation de E Brassine: En résumé , par la première question 125-64 = x3 + y3 , par la troisième Bachet trouveque 125-64 = 15252992 / 250047 - 125 / 250047, on peut donc se proposer de résoudre 15252992 / 250047 - 125 / 250047=x3 + y3, qui d'aprés la forme du premier nombre donnera pour x et y une solution nouvelle Brassine n'en dit pas plus , la recurence des deux fonctions ne donnant rien , rétirer 2b3 a a3 + b3 ne donnant aussi pas grand chose, il nous faut aborder la methode employée dans la suite : l'observation de Fermat sur la Troisième question , C'est à dire l'échange des dénominateurs:
Aprés de nombreuses recherches intensives , et en m'inspirant de l'observation de Fermat sur la Troisième question , qui nous guide dans la démarche de Pierre de Fermat quant à la manière dont il réalise Q1 = Q3 sans faire Q1 ° Q3 mais en réalisant Q1=x=Q2, je propose la démonstation suivante correspondante à la diférence de 60 et 125 et à la suite de ses notes quant à la boucle entre Q1 et Q2 et Q3. Si nous considérons que
Pour obtenir une double égalité, si
Avec la différence des deux cubes 64 et 125 nous avons construit deux cubes 64 (43) et 13 dont la somme égale la différence de deux nombres 60 et 125 pouvant être élevés au cube pour entrer dans Q1. L'on note que Il est clair que pour batir sa démonstration Fermat ne s'est pas seulement appuyé sur un exemple numèrique, il nous reste à batir une généralisation de cette théorie aboutissant à sa note du livre II question 10 et au GTF à savoir:
Livre IV,Question I et II , Sous Question 3 de Bachet
OBSERVATION DE FERMAT SUR LA TROISIEME QUESTION.( La méthode qu'emploi Bachet pour cette troisième question n'est pas légitime, et nous l'apercevrons par un procédé pareil à celui dont nous avons fait usage pour la première question. ( De plus, par ce qui à été dit ci dessus , nous construirons aisément une question que Bachet à ignorée. Diviser un nombre donné composé de deux cubes en deux autres cubes, et cela par une suite infinie d'opérations successives, comme nous l'avons indiqué plus haut.
Une piste complémentaire pour le cube de 60 et la fameuse démonstration qui étonnerait Bachet nous est donné dans la manière dont Fermat trouve ces deux cubes. Raprochons ces deux cubes
D'autre part , nous avons observé au chapitre précédent que Remplaçons 53 + 43 dans Déplaçons le 33 vers le dénominateur :
|
||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
En janvier 2013, aprés avoir reconstitué toutes ces équations, j'en conclus que ces seules démonstrations ne suffisent pas à conduire sur la piste du Grand Théorème de Fermat et qu'il faut aller chercher encore plus loin, c'est à dire d'orienter mes recherches vers le livre II... (avril 2013!!!)

Patrick Stoltz le 181/0/2012 - 4/12/2012 - 22/01/2013 pstoltz@shemath.com
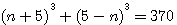
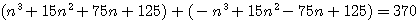
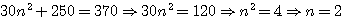
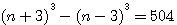
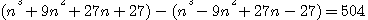
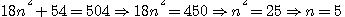
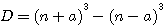
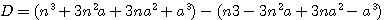
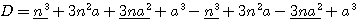
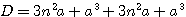
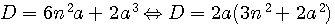
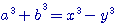 )
)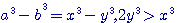 )
)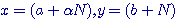 , en disposant
, en disposant 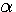 de manière à faire disparaître , après la substitution , la première puissance de N; on tombe alors sur une relation de la forme
de manière à faire disparaître , après la substitution , la première puissance de N; on tombe alors sur une relation de la forme 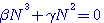 qui donne de suite
qui donne de suite 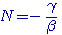 ..
..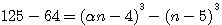 ,la méthode de généralisation de Fermat, et la note de Emile Brassine. (qui produisent les cubes
,la méthode de généralisation de Fermat, et la note de Emile Brassine. (qui produisent les cubes 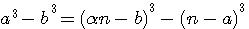
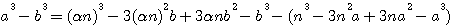
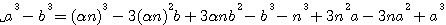
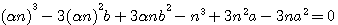
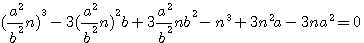
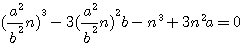
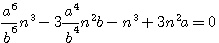
 pour faire disparaître par substitution la première puissance de
pour faire disparaître par substitution la première puissance de 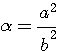
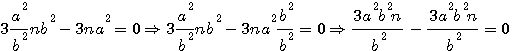
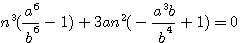
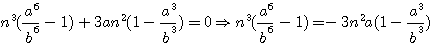
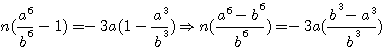
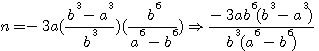
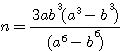
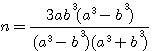
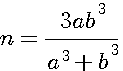
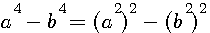
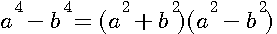
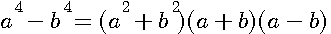
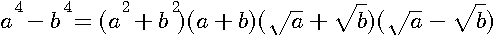
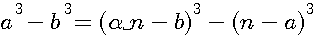
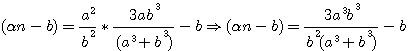
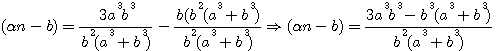
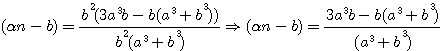
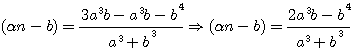
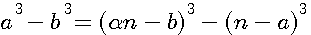
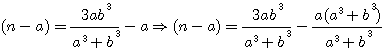
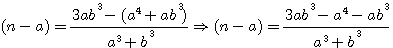
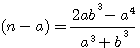
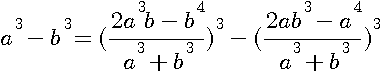
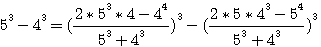
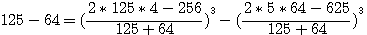
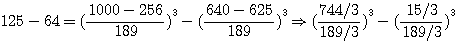
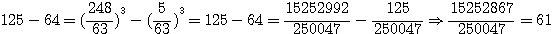
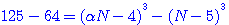 ce qui donne, en faisant disparaître la première puissance de N par le moyen de l'indéterminée
ce qui donne, en faisant disparaître la première puissance de N par le moyen de l'indéterminée 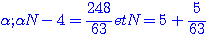
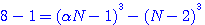 , et alors on aurait trouvé
, et alors on aurait trouvé 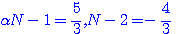
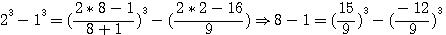
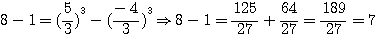
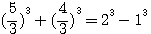 ,
,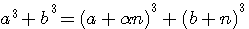
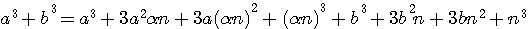
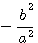
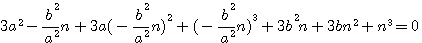
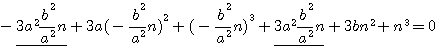
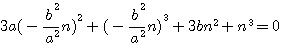
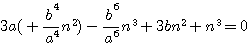
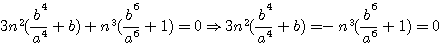
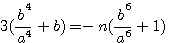
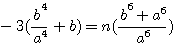
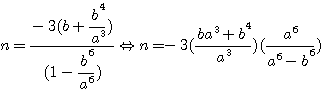
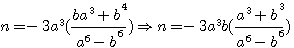
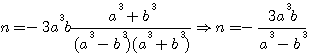
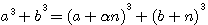
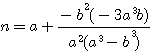
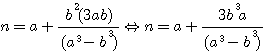
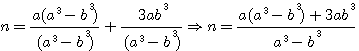 =>
=>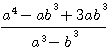
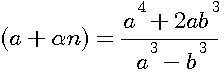
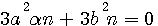
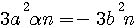 =>
=> 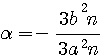 =>
=> 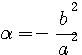
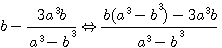
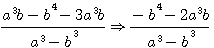
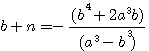
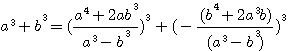 ou puisqu'au cube
ou puisqu'au cube 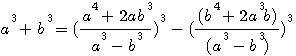
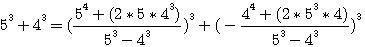
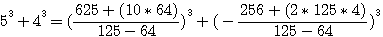
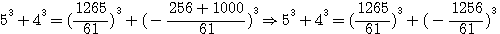
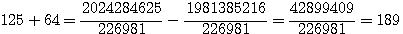
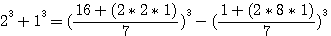
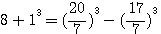
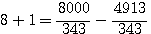
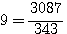
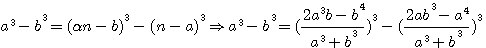
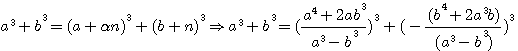
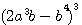 factorisons b :
factorisons b :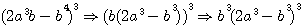
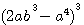 , factorisons a
, factorisons a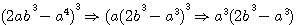
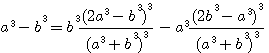
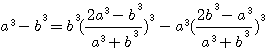
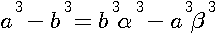
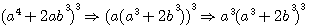
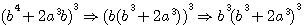
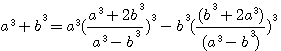
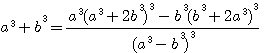
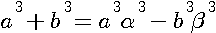
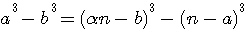
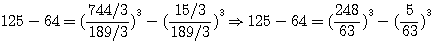
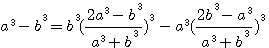
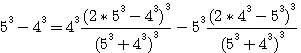
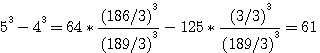
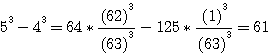 ,notez que 4*62 est bien = à 744 (voir rappel ci dessus), 5
,notez que 4*62 est bien = à 744 (voir rappel ci dessus), 5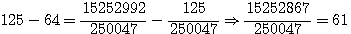
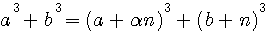
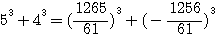
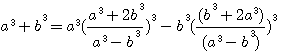
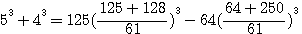
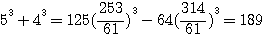
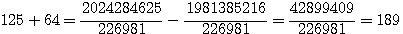
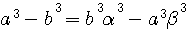 , la SOMME des numérateurs de
, la SOMME des numérateurs de 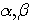 =
= 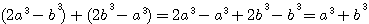 , étant égale au dénominateur de
, étant égale au dénominateur de 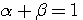 .
.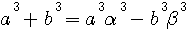 , la DIFFERENCE des numérateurs de
, la DIFFERENCE des numérateurs de 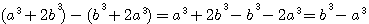 , étant égale à l'opposé du dénominateur de
, étant égale à l'opposé du dénominateur de 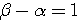
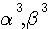 ou
ou 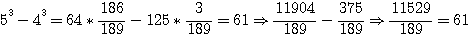
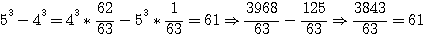
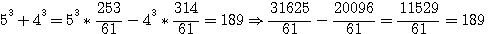
 ) , peuvent être transposés à la première question (
) , peuvent être transposés à la première question (  ) puisque le double du plus petit ne surpasse pas le plus grand.
) puisque le double du plus petit ne surpasse pas le plus grand. )
)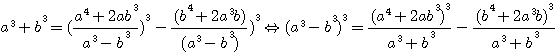
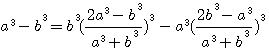
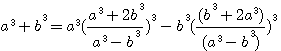
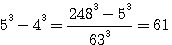 , et que
, et que 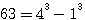 alors nous pouvons chercher une solution pour
alors nous pouvons chercher une solution pour 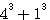 avec au dénominateur de Q3
avec au dénominateur de Q3 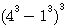
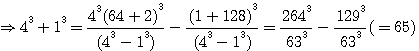
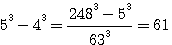 alors
alors 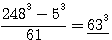 ET SI
ET SI 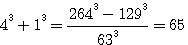 alors
alors 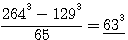
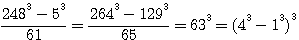
 )
) )
)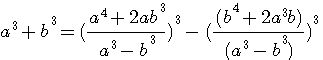
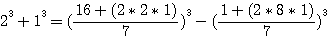
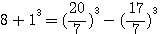
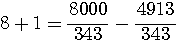
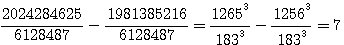 trouvés par Fermat avec les deux cubes de Q3
trouvés par Fermat avec les deux cubes de Q3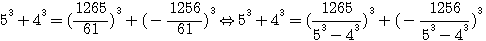
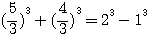 Donc
Donc 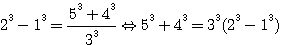
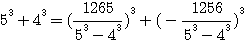 par 3
par 3