En bleu les annotations de

Diophante.

En vert les annotations de

Fermat.

En bleu marine

Emile Brassine

Sur fond jaune, des notes importantes et les calculs réalisés avec les équations retrouvés avec les nombres donnés en exemple dans les notes de Fermat

Comment Diophante trouve 16/5?

Les 16 s'annulent, -n²=4n² devient 5n²

L'on note que:

20/5 - 16/5 =4/5 ,et que 20/5 - 12/5 = 8/5 le double de l'écart

Le dénominateur ,bien sûr, NE S'ADDITIONNE PAS

Nouvelle question : diviser l'unité en 2 Carrés

Je rajoute une question sur le même modéle (prémice de la question XII du livre V):

Diviser l'unité en deux carrés : soit l'unité (égal 1) j'appellerai N² et 1-N² les carrés cherchés , il reste à trouver N de telle sorte que 1 - N² soit un carré , Je pose 1-N² = (2n-1)² d'où n=4/5

Remplaçons n par sa valeur dans (2n-1)²

La surface de ce triangle égale (3/5*4/5)/2 = 6/25

Mais aussi  : 1 + (4/3)² = (5/3)²   ou    (3/4)² + 1 = (5/4)²

Cette nouvelle question est le prémice de la question 12 du livre V

Extrait d'une lettre de Fermat à Roberval:

...mais voici ce que j'ai découvert depuis sur le sujet de la proposition 12 du Véme livre de Diophante ; en quoi j'ai suppléé ce que Bachet avoue n'avoir su , et rétabli en même temps la corruption du texte deDiophante ; ce qui serait trop long à vous déduire. Il suffit que vous voyiez ma proposition, et que je vous fasse plutôt souvenir que j'ai autrefois démontré qu'un nombre moindre de l'unité qu'un multiple du quaternaire (4n-1) , n'est ni un carré , ni composé de deux carrés , ni en entier , ni en fraction ...

Remarque sur la question 31 Livre IV

Reprenons l'exemple de la question 31 du livre 4 : diviser 3² en deux carrés en multipliant chaque cotés de ce triangle par le coté de 3² c'est à dire 3.

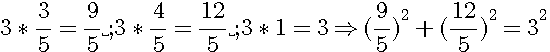
verification : 81/25 + 144/25 = 225/25=9

Observation de Fermat, le Grand Thèorème de Fermat :

Décomposer un cube en deux autres cubes, une quatrièmes puissance quelconque en deux puissances de même nom au dessus de la deuxième puissance, est une chose impossible, et j'en ai assurément trouvé l'admirable démonstration, la marge trop exiguë ne la contiendrait pas.

Remarque: Comme confirmé dans d'autres annnotations , Fermat ne parlait pas seulement des nombres entiers mais de rationnels et ou premiers ou non.

Pour preuve son observation dans la question XXII du livre III : ... seule fois l'hypoténuse d'un triangle rectangle (formé de cotè entiers), son carré deux fois ...

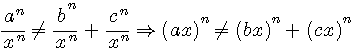
Livre II question 10 Diviser un nombre qui est la somme de deux carrés en deux autres carrés

Diviser un nombre qui est la somme de deux carrés en deux autres carrés.

Exemple: soit le nombre donné 13=4+9 , j'appelle (2+N)² et (2N - 3)² les deux carrés cherchés; un devra avoir 4+9=(2+N)² + (2N - 3)² d'ou N = 8/5

Un nombre composé de la somme de deux cubes ne pourrait-il pas être décomposé en deux autres cubes? Cette question difficile n'a pas été assurément connus de Viele, de Bachet, et peut être même de Diophante, j'en ai cependant donné la solution dans les notes, à la deuxième question du livre IV

D'aprés cette note de Fermat située juste au probléme suivant , l'on peut raisonablement considérer que Fermat avait déjà étudié le Livre IV (question II)  AVANT d'affirmer son admirable demonstration . De plus, en étudiant un bon nombre de questions et d'annotations de Fermat ,que je détaille ci dessous, Il fait souvent référence à ses théorèmes enoncés sur des questions postèrieures .

Par exemple , les hypoténuses 4n+1 sont évoquées entre autre dans le Livre III question 22 et , Livre V question 12